给定唯一的结果
唯一的结果 时间:2021-05-25 阅读:()
第36卷第2期江西师范大学学报(自然科学版)Vol.
36No.
22012年3月JournalofJiangxiNormalUniversity(NaturalScience)Mar.
2012收稿日期:2011-11-15基金项目:国家自然科学基金(10921101)资助项目.
作者简介:宋丽(1979-),女,四川新津人,副教授,博士研究生,主要从事金融数学与金融工程的研究.
文章编号:1000-5862(2012)02-0160-05一类具有一致连续系数的倒向重随机微分方程宋丽1,2(1.
山东轻工业学院财政与金融学院,山东济南250100;2.
山东大学数学学院,山东济南250100)摘要:利用倒向重随机微分方程解的比较定理和函数逼近方法讨论了一类具有一致连续系数的1维倒向重随机微分方程,得到了此类方程解的存在定理,推广了系数满足Lipschitz条件的情形.
关键词:倒向重随机微分方程;倒向随机积分;存在定理中图分类号:O211.
63文献标志码:A0引言1990年,E.
Pardoux等[1]提出了如下形式的倒向随机微分方程(BSDE):(,,)dd(0),TTtssssttYfsYZsZBtTξ=+∫∫≤≤在生成元f关于变量y与z是Lipschitz的,终端条件ξ和[0,]((,0,0))tTft∈是平方可积的条件下,证明了此类非线性BSDEs存在唯一的一对适应的平方可积解[0,](,)tttTYZ∈.
正是由于倒向随机微分方程在随机控制、金融数学、随机博弈等领域有着广泛应用,从此许多学者致力于研究在各种不同条件下,BSDEs解的存在性[2-5].
1994年,E.
Pardoux等[6]引入了倒向重随机微分方程(BDSDE).
它是倒向随机微分方程的一个重要推广形式,在系数,fg满足Lipschitz条件下,文献[6]已证明了解的存在唯一性结果.
ShiYu-feng等[7]于2005年证明了BDSDE解的比较定理,并指出利用此比较定理可以证明在一定连续条件下,BDSDE解的存在性,但并未进行具体证明.
关于在非Lipschitz条件下,BDSDE解的存在性讨论可以参见文献[8-10].
本文主要利用文献[9]中更弱条件下的比较定理,证明一类具有一致连续系数的BDSDEs解的存在性.
1预备知识和引理首先引入一些记号、假设和引理.
设(,,)FPΩ是一个完备概率空间,T是一个给定的正实数,{},0tWtT,0tBtT≤≤是2个定义在(,,FΩ)P上分别取值于dR和lR的互相独立的标准Brown运动.
令N是F中所有P-零集构成的集合,[0,t∈]T,定义,:WBtttTFFF=∨,对任意的随机过程{},tη{},0,;,rsttTtFsrtNFFηηησηη=∨=≤≤.
显然{,tF}[0,]tT∈既不是递增的,也不是递减的,因此它不能构成经典的信息流.
对任意正整数d,dx∈R,记其欧几里得范数为*||xxx=,其中*x是x的转置.
定义如下过程空间:{}22220([0,,:sup;ttstTSTFE==,使得12[0,],,tTyy∈∈12,,,dzz∈RR有112212ftyzftyzKyy≤12|||);zz+(H4)2(,0,0)(0,;)fMT∈R;(H5)存在2个连续、次可加、非减的非负函数和:ψ++→RR,使得1212[0,dtTyyzz∈∈∈RR,有11221212ftyzftyzyyzzψ+≤这里和ψ满足:x+∈R,01xxKψ++≤≤)x,且(0)(0)0ψ==.
给定2TLFPξΩ∈R,下面考虑如下形式的BDSDEsfgTξ:(,,)d(,,)dd(0),TtsstTTssSssttYfsYZsgsYZBZWtTξ=++∫1)其中关于{}tB的积分为倒向It积分,关于{}tW的积分为标准正向It积分,这2类积分都是It-Skorohod积分的特殊类型[11].
定义1给定2TLFPξΩ∈R,称一对随机过程(,)YZ为方程(1)的解,如果它满足(1)式并且有22(,)([0,];)(0,;)dYZSTMT∈*RR.
引理1如果给定2TLFPξΩ∈R,则在(H1)~(H4)假设条件下,方程(1)存在唯一解22(,)([0,];)(0,;)dYZSTMT∈*RR.
引理2给定122TLFPξξΩ∈R,g满足(H1)~(H2),12,ff满足(H3)~(H4),1122YZYZ分别是11111111(,,)d(,,)dd(0),TtsstTTssSssttYfsYZsgsYZBZWtTξ=++∫∫∫≤≤22222222(,,)d(,,)dd(0)TtsstTTssSssttYfsYZsgsYZBZWtTξ=++∫∫∫≤≤的解,如果终端条件12ξξ≤并且222211111212ttttttttftYZftYZftYZftYZ≤或≤则12,ttYYt∈≤[0,]T.
2主要结果定理1如果g满足(H1)~(H2),f满足(H4)~(H5),给定2TLFPξΩ∈R,则方程(1)存在解(,)YZ∈22([0,];)(0,;)dSTMT*RR.
对于条件(H5)中的函数和ψ,将其延拓为和:ψ→RR,即000)xxxxII时,假设112,(,,nininitttttYyyYfty≤≤≤2)(0,;)nitzMT∈R,考虑如下BDSDE:111111(||)]d(,,)dd(0).
TnininininitssnsstTninininssstTninisssstyfsyzyyzzsgsyzBzWtTξΦΨ+++++++∫∫∫≤≤(3)因为12nitttYyY≤≤,类似于2i=的情形,可得222221111(||).
ninittnttnttnininittttnttninttftYZYyZzftyzftYZyYzZΦΨΦΨ++≥≥(4)令1ninininittntnftyzftyzyyzΦΨ+|)nitz,则易验证1nif+满足(H4)和(H5),且1222222211111ninininittttnttninttttnininininittttttninininininttnttttftYZftyzYyZzftYZftyzftyzftYZyYzZftyzΦΨΦΨ++===≤≥因此,同样由引理1和引理2可得,当2i>时,方程(3)存在唯一解11(,)niniyz++且112ninittttYyyY+≤≤≤,[0,]tT∈.
引理3得证.
引理4若g满足(H1)~(H2),f满足(H4)~(H5),则对任意给定的n≥1,2200supsup||||dTninittitTEyzt+<∞∫≤≤.
证由引理3的结论得,对任意给定的1n≥,有21200220supsup||sup||sup||.
nittitTtTttTEyEYEY+<∞≤≤≤≤≤≤≤由(4)式和(a1)可得11111211163nininininittttnininininttnttjjjjjttttjninininittttftyzftyzyyzzKftYZKYZKyzKyzΦΨ+++++=+++++++++++∑≤≤(5)对12||nity+应用It公式,并对(5)式两端取数学期望得1221100111120||d||2(,,)dd.
TTnininitttTninininittttEztEEyftyztEgtyztξ++++++++*+∫∫∫≤由(H1)和不等式22()1(1)/(2)abaαα+++≤[]2[12/(1)]bαα+得第2期宋丽:一类具有一致连续系数的倒向重随机微分方程16311211221211221(,0,0)|1|(,0,0)|||12ninininittttnitgtyzgtyzgtgtKyαααααα++++++++++≤≤122110,0)|21nitzgtααα++++.
(6)由(5)~(6)式和Young不等式[12]得1220001201||d||d83||d,4TTninittTnitEztCEztEztαα+++++∫∫∫≤其中210012||(6sup176d221TnijjtjttijjjttCEyKftYZKKYZtKKααα+==+++∑∫12100||d6||||dTTnininitttytKyyt+++*+∫∫22010,0)|d.
1TEEgttαξα++∫因此12200041||d||d12TTninittCEztEztα++∫∫≤.
所以2200supsupdTninittitTEyzt+<∞∫≤≤.
引理4得证.
引理5对任意给定的1n≥,存在过程(,ny22)([0,];)(0,;)nzSTMT∈*RR满足2200||||d0()supTninninttttTEyyzzti∫≤≤.
证对任意给定的1n≥,由引理3知,nity关于i是单调的,因此,2([0,];)nyST∈R使得nity→()ntyi→∞,且20[||]supnttTEy<∞≤≤.
由控制收敛定理得20||d0()TninttEyyti→→∞∫.
由(5)式得210dsupTnininittiCEftyzt=<∞∫.
(7)对2||ninjttyy应用It公式,并两端取数学期望,由Hlder不等式、(H1)和(7)式得220||||dTninjninjttttEyyEzzt+∫≤{}02dTninjninininjnjnjttttttEyyftyzftyzt+∫{}{201/2200d2||dTnininjnjttttTTninjnininittttEgtyzgtyztEyytEftyz∫∫∫≤}1/22200|d||d|TTnjninjnitttftKEyytEzα∫∫{}1/222102200|d4||d||d||d.
TnjninjtttTTninjninjttttztCEyytKEyytEzztα++∫∫∫≤因此有{}12001/22204||d|1|d||d,1TTninjnitttTnjninjtttCEzztEyKytEyytαα+∫∫∫≤故{}1nitiz∞=是2(0,;)MTR中的Cauchy列,所以nz∈2(0,;)MTR使得20||d0().
TninttEzzti→→∞∫引理5得证.
在方程(2)两端令i→∞,得0)(0)]d(,,)dd(0),TnnntssnntTTnnnsssssttyfsyzsgsyzBzWtTξΦΨ∫8)即对任意给定的1n≥nnyz是方程(8)的解.
定理1的证明首先证明112nnttttYyyY+≤≤≤,[0,]tT∈.
由引理3得12ntttYyY≤≤,下证nty≤1nty+.
根据方程(8)可得11111(0)(0)(0)(0)]d[(,,TnnnnnnttsssstTnnnnnstyyfsyzfsyzsgsyΦΦΨΨ+++++=+++∫∫111d()dTnnnnnssssssstzgsyzBzzW+++=∫11dTnnnnnnssnsstyyzzsΔΦΨ++∫111d()d(0),TnnnnssssstTnnssstgsyzgsyzBzzWtT+++∫∫≤≤其中1111110)(0)(0)(0)nnnnnssssnnnnnnnnnssnssfsyzfsyzyyzzΔΦΦΨΨΦΨ++++++由(A2)和(H5)得164江西师范大学学报(自然科学版)2012年1111nnnnssssnnnnnssnssfsyzfsyzyyzzΦΨ++++≤所以0nΔ≤.
由引理2可得10nnttyy+≤,即112nnttttYyyY+≤≤≤.
所以{}1ntny∞=在2([0,];)STR中收敛,记其极限为Y,并且有20221200supsupsupsup.
ntntTtttTtTEyEYEY+<∞≤≤≤≤≤≤≤下面证明{}1ntiz∞=是2(0,;)dMTR中的Cauchy列.
记0)(0),nnnnnttttnnftyzftyzΦΨ=由(A3)和(a1)得0)||(0)|nnnnnttttnnftyzftyzΦΨ++≤≤120)||(0)|nnnnttttnnftyzftyzΦΨ+++≤11|2(,0,0)|2(||)20)||(0)|nnttnnftyzΦΨΦΨ|2(,0,0)|420)||(0)|nnttnnftKKyzΦΨ类似于引理4的证明可得20sup||dTntnEzt<∞∫.
类似于引理5的证明可得{}1ntnz∞=是2(0,M;)dTR中的Cauchy列,记其极限为Z,在(8)式两端令n→∞,由g的连续性和(a4)可得000(,)d(,)dd(0),TTtsssssTssYfYZsgYZBZWtTξ=++∫∫∫≤≤即(,)YZ是方程(1)的解.
3参考文献[1]PardouxE,PengShige.
Adaptedsolutionofabackwardstochasticdifferentialequation[J].
SystemsControlLett,1990,14(1):55-61.
[2]LepeltierJP,MartinJS.
Backwardstochasticdifferentialequa-tionswithcontinuouscoefficient[J].
StatisticandProbabilityLetters,1997,32(4):425-430.
[3]TianDejian,JiangLong,DavisonM.
Ontheexistenceofsolu-tionstoBSDEswithgeneralizeduniformlycontinuousgenerators[J].
StatisticandProbabilityLetters,2010,80(9/10):903-909.
[4]HamadèneS.
Multidimensionalbackwardstochasticdifferentialequationswithuniformlycontinuouscoeffcients[J].
Bernoulli,2003,9(3):517-534.
[5]JiaGuangyan.
Aclassofbackwardstochasticdifferentialequa-tionswithdiscontinuouscoefficients[J].
StatisticandProbabilityLetters,2008,78(3):231-237.
[6]PardouxE,PengShige.
BackwarddoublystochasticdifferentialequationsandsystemsofquasilinearSPDEs[J].
ProbabTheoryRelatFields,1994,98(2):209-227.
[7]ShiYufeng,GuYanling,LiuKai.
Comparisontheoremsofbackwarddoublystochasticdifferentialequationsandapplications[J].
StochasticAnalysisandApplication,2005,23(1):97-110.
[8]LinQian.
Aclassofbackwarddoublystochasticdifferentialequationswithnon-Lipschitzcoeffcients[J].
StatisticandProb-abilityLetters,2009,79(20):2223-2229.
[9]LinQian.
Ageneralizedexistencetheoremofbackwarddoublystochasticdifferentialequations[J].
ActaMathematicaSinica:EnglishSeries,2010,26(8):1525-1534.
[10]朱波,韩宝燕.
非Lipschitz条件下的倒向重随机微分方程[J].
数学物理学报,2008,28A(5):977-984.
[11]NaulartD,PardouxE.
Stochasticcalculuswithanticipatinginte-grands[J].
ProbabTheoryRelatFields,1988,78(4):535-581.
[12]马戈,堃黄.
半线性抛物方程各向异性有限元逼近[J].
江西师范大学学报:自然科学版,2010,34(5):480-483,494.
AClassofBDSDEswithUniformlyContinuousCoefficientsSONGLi1,2(1.
SchoolofFinance,ShandongLightIndustrySchool,Ji'nanShandong250100,China;2.
SchoolofMathematics,ShandongUniversity,Ji'nanShandong250100,China)Abstract:Bycomparisontheoremofbackwarddoublystochasticdifferentialequationsandapproximationoffunction,aclassofone-dimensionalbackwarddoublystochasticdifferentialequations(BDSDEs)isstudied,wherethecoefficientsisuniformlycontinuous.
AnexistencetheoremforsolutionsoftheclassofBDSDEsisobtained,whichgeneralizesthesituationthatthecoefficientsatisfyLipschitzconditions.
Keywords:backwarddoublystochasticdifferentialequation;backwardstochasticintegral;existencetheorem(责任编辑:曾剑锋)
36No.
22012年3月JournalofJiangxiNormalUniversity(NaturalScience)Mar.
2012收稿日期:2011-11-15基金项目:国家自然科学基金(10921101)资助项目.
作者简介:宋丽(1979-),女,四川新津人,副教授,博士研究生,主要从事金融数学与金融工程的研究.
文章编号:1000-5862(2012)02-0160-05一类具有一致连续系数的倒向重随机微分方程宋丽1,2(1.
山东轻工业学院财政与金融学院,山东济南250100;2.
山东大学数学学院,山东济南250100)摘要:利用倒向重随机微分方程解的比较定理和函数逼近方法讨论了一类具有一致连续系数的1维倒向重随机微分方程,得到了此类方程解的存在定理,推广了系数满足Lipschitz条件的情形.
关键词:倒向重随机微分方程;倒向随机积分;存在定理中图分类号:O211.
63文献标志码:A0引言1990年,E.
Pardoux等[1]提出了如下形式的倒向随机微分方程(BSDE):(,,)dd(0),TTtssssttYfsYZsZBtTξ=+∫∫≤≤在生成元f关于变量y与z是Lipschitz的,终端条件ξ和[0,]((,0,0))tTft∈是平方可积的条件下,证明了此类非线性BSDEs存在唯一的一对适应的平方可积解[0,](,)tttTYZ∈.
正是由于倒向随机微分方程在随机控制、金融数学、随机博弈等领域有着广泛应用,从此许多学者致力于研究在各种不同条件下,BSDEs解的存在性[2-5].
1994年,E.
Pardoux等[6]引入了倒向重随机微分方程(BDSDE).
它是倒向随机微分方程的一个重要推广形式,在系数,fg满足Lipschitz条件下,文献[6]已证明了解的存在唯一性结果.
ShiYu-feng等[7]于2005年证明了BDSDE解的比较定理,并指出利用此比较定理可以证明在一定连续条件下,BDSDE解的存在性,但并未进行具体证明.
关于在非Lipschitz条件下,BDSDE解的存在性讨论可以参见文献[8-10].
本文主要利用文献[9]中更弱条件下的比较定理,证明一类具有一致连续系数的BDSDEs解的存在性.
1预备知识和引理首先引入一些记号、假设和引理.
设(,,)FPΩ是一个完备概率空间,T是一个给定的正实数,{},0tWtT,0tBtT≤≤是2个定义在(,,FΩ)P上分别取值于dR和lR的互相独立的标准Brown运动.
令N是F中所有P-零集构成的集合,[0,t∈]T,定义,:WBtttTFFF=∨,对任意的随机过程{},tη{},0,;,rsttTtFsrtNFFηηησηη=∨=≤≤.
显然{,tF}[0,]tT∈既不是递增的,也不是递减的,因此它不能构成经典的信息流.
对任意正整数d,dx∈R,记其欧几里得范数为*||xxx=,其中*x是x的转置.
定义如下过程空间:{}22220([0,,:sup;ttstTSTFE==,使得12[0,],,tTyy∈∈12,,,dzz∈RR有112212ftyzftyzKyy≤12|||);zz+(H4)2(,0,0)(0,;)fMT∈R;(H5)存在2个连续、次可加、非减的非负函数和:ψ++→RR,使得1212[0,dtTyyzz∈∈∈RR,有11221212ftyzftyzyyzzψ+≤这里和ψ满足:x+∈R,01xxKψ++≤≤)x,且(0)(0)0ψ==.
给定2TLFPξΩ∈R,下面考虑如下形式的BDSDEsfgTξ:(,,)d(,,)dd(0),TtsstTTssSssttYfsYZsgsYZBZWtTξ=++∫1)其中关于{}tB的积分为倒向It积分,关于{}tW的积分为标准正向It积分,这2类积分都是It-Skorohod积分的特殊类型[11].
定义1给定2TLFPξΩ∈R,称一对随机过程(,)YZ为方程(1)的解,如果它满足(1)式并且有22(,)([0,];)(0,;)dYZSTMT∈*RR.
引理1如果给定2TLFPξΩ∈R,则在(H1)~(H4)假设条件下,方程(1)存在唯一解22(,)([0,];)(0,;)dYZSTMT∈*RR.
引理2给定122TLFPξξΩ∈R,g满足(H1)~(H2),12,ff满足(H3)~(H4),1122YZYZ分别是11111111(,,)d(,,)dd(0),TtsstTTssSssttYfsYZsgsYZBZWtTξ=++∫∫∫≤≤22222222(,,)d(,,)dd(0)TtsstTTssSssttYfsYZsgsYZBZWtTξ=++∫∫∫≤≤的解,如果终端条件12ξξ≤并且222211111212ttttttttftYZftYZftYZftYZ≤或≤则12,ttYYt∈≤[0,]T.
2主要结果定理1如果g满足(H1)~(H2),f满足(H4)~(H5),给定2TLFPξΩ∈R,则方程(1)存在解(,)YZ∈22([0,];)(0,;)dSTMT*RR.
对于条件(H5)中的函数和ψ,将其延拓为和:ψ→RR,即000)xxxxII时,假设112,(,,nininitttttYyyYfty≤≤≤2)(0,;)nitzMT∈R,考虑如下BDSDE:111111(||)]d(,,)dd(0).
TnininininitssnsstTninininssstTninisssstyfsyzyyzzsgsyzBzWtTξΦΨ+++++++∫∫∫≤≤(3)因为12nitttYyY≤≤,类似于2i=的情形,可得222221111(||).
ninittnttnttnininittttnttninttftYZYyZzftyzftYZyYzZΦΨΦΨ++≥≥(4)令1ninininittntnftyzftyzyyzΦΨ+|)nitz,则易验证1nif+满足(H4)和(H5),且1222222211111ninininittttnttninttttnininininittttttninininininttnttttftYZftyzYyZzftYZftyzftyzftYZyYzZftyzΦΨΦΨ++===≤≥因此,同样由引理1和引理2可得,当2i>时,方程(3)存在唯一解11(,)niniyz++且112ninittttYyyY+≤≤≤,[0,]tT∈.
引理3得证.
引理4若g满足(H1)~(H2),f满足(H4)~(H5),则对任意给定的n≥1,2200supsup||||dTninittitTEyzt+<∞∫≤≤.
证由引理3的结论得,对任意给定的1n≥,有21200220supsup||sup||sup||.
nittitTtTttTEyEYEY+<∞≤≤≤≤≤≤≤由(4)式和(a1)可得11111211163nininininittttnininininttnttjjjjjttttjninininittttftyzftyzyyzzKftYZKYZKyzKyzΦΨ+++++=+++++++++++∑≤≤(5)对12||nity+应用It公式,并对(5)式两端取数学期望得1221100111120||d||2(,,)dd.
TTnininitttTninininittttEztEEyftyztEgtyztξ++++++++*+∫∫∫≤由(H1)和不等式22()1(1)/(2)abaαα+++≤[]2[12/(1)]bαα+得第2期宋丽:一类具有一致连续系数的倒向重随机微分方程16311211221211221(,0,0)|1|(,0,0)|||12ninininittttnitgtyzgtyzgtgtKyαααααα++++++++++≤≤122110,0)|21nitzgtααα++++.
(6)由(5)~(6)式和Young不等式[12]得1220001201||d||d83||d,4TTninittTnitEztCEztEztαα+++++∫∫∫≤其中210012||(6sup176d221TnijjtjttijjjttCEyKftYZKKYZtKKααα+==+++∑∫12100||d6||||dTTnininitttytKyyt+++*+∫∫22010,0)|d.
1TEEgttαξα++∫因此12200041||d||d12TTninittCEztEztα++∫∫≤.
所以2200supsupdTninittitTEyzt+<∞∫≤≤.
引理4得证.
引理5对任意给定的1n≥,存在过程(,ny22)([0,];)(0,;)nzSTMT∈*RR满足2200||||d0()supTninninttttTEyyzzti∫≤≤.
证对任意给定的1n≥,由引理3知,nity关于i是单调的,因此,2([0,];)nyST∈R使得nity→()ntyi→∞,且20[||]supnttTEy<∞≤≤.
由控制收敛定理得20||d0()TninttEyyti→→∞∫.
由(5)式得210dsupTnininittiCEftyzt=<∞∫.
(7)对2||ninjttyy应用It公式,并两端取数学期望,由Hlder不等式、(H1)和(7)式得220||||dTninjninjttttEyyEzzt+∫≤{}02dTninjninininjnjnjttttttEyyftyzftyzt+∫{}{201/2200d2||dTnininjnjttttTTninjnininittttEgtyzgtyztEyytEftyz∫∫∫≤}1/22200|d||d|TTnjninjnitttftKEyytEzα∫∫{}1/222102200|d4||d||d||d.
TnjninjtttTTninjninjttttztCEyytKEyytEzztα++∫∫∫≤因此有{}12001/22204||d|1|d||d,1TTninjnitttTnjninjtttCEzztEyKytEyytαα+∫∫∫≤故{}1nitiz∞=是2(0,;)MTR中的Cauchy列,所以nz∈2(0,;)MTR使得20||d0().
TninttEzzti→→∞∫引理5得证.
在方程(2)两端令i→∞,得0)(0)]d(,,)dd(0),TnnntssnntTTnnnsssssttyfsyzsgsyzBzWtTξΦΨ∫8)即对任意给定的1n≥nnyz是方程(8)的解.
定理1的证明首先证明112nnttttYyyY+≤≤≤,[0,]tT∈.
由引理3得12ntttYyY≤≤,下证nty≤1nty+.
根据方程(8)可得11111(0)(0)(0)(0)]d[(,,TnnnnnnttsssstTnnnnnstyyfsyzfsyzsgsyΦΦΨΨ+++++=+++∫∫111d()dTnnnnnssssssstzgsyzBzzW+++=∫11dTnnnnnnssnsstyyzzsΔΦΨ++∫111d()d(0),TnnnnssssstTnnssstgsyzgsyzBzzWtT+++∫∫≤≤其中1111110)(0)(0)(0)nnnnnssssnnnnnnnnnssnssfsyzfsyzyyzzΔΦΦΨΨΦΨ++++++由(A2)和(H5)得164江西师范大学学报(自然科学版)2012年1111nnnnssssnnnnnssnssfsyzfsyzyyzzΦΨ++++≤所以0nΔ≤.
由引理2可得10nnttyy+≤,即112nnttttYyyY+≤≤≤.
所以{}1ntny∞=在2([0,];)STR中收敛,记其极限为Y,并且有20221200supsupsupsup.
ntntTtttTtTEyEYEY+<∞≤≤≤≤≤≤≤下面证明{}1ntiz∞=是2(0,;)dMTR中的Cauchy列.
记0)(0),nnnnnttttnnftyzftyzΦΨ=由(A3)和(a1)得0)||(0)|nnnnnttttnnftyzftyzΦΨ++≤≤120)||(0)|nnnnttttnnftyzftyzΦΨ+++≤11|2(,0,0)|2(||)20)||(0)|nnttnnftyzΦΨΦΨ|2(,0,0)|420)||(0)|nnttnnftKKyzΦΨ类似于引理4的证明可得20sup||dTntnEzt<∞∫.
类似于引理5的证明可得{}1ntnz∞=是2(0,M;)dTR中的Cauchy列,记其极限为Z,在(8)式两端令n→∞,由g的连续性和(a4)可得000(,)d(,)dd(0),TTtsssssTssYfYZsgYZBZWtTξ=++∫∫∫≤≤即(,)YZ是方程(1)的解.
3参考文献[1]PardouxE,PengShige.
Adaptedsolutionofabackwardstochasticdifferentialequation[J].
SystemsControlLett,1990,14(1):55-61.
[2]LepeltierJP,MartinJS.
Backwardstochasticdifferentialequa-tionswithcontinuouscoefficient[J].
StatisticandProbabilityLetters,1997,32(4):425-430.
[3]TianDejian,JiangLong,DavisonM.
Ontheexistenceofsolu-tionstoBSDEswithgeneralizeduniformlycontinuousgenerators[J].
StatisticandProbabilityLetters,2010,80(9/10):903-909.
[4]HamadèneS.
Multidimensionalbackwardstochasticdifferentialequationswithuniformlycontinuouscoeffcients[J].
Bernoulli,2003,9(3):517-534.
[5]JiaGuangyan.
Aclassofbackwardstochasticdifferentialequa-tionswithdiscontinuouscoefficients[J].
StatisticandProbabilityLetters,2008,78(3):231-237.
[6]PardouxE,PengShige.
BackwarddoublystochasticdifferentialequationsandsystemsofquasilinearSPDEs[J].
ProbabTheoryRelatFields,1994,98(2):209-227.
[7]ShiYufeng,GuYanling,LiuKai.
Comparisontheoremsofbackwarddoublystochasticdifferentialequationsandapplications[J].
StochasticAnalysisandApplication,2005,23(1):97-110.
[8]LinQian.
Aclassofbackwarddoublystochasticdifferentialequationswithnon-Lipschitzcoeffcients[J].
StatisticandProb-abilityLetters,2009,79(20):2223-2229.
[9]LinQian.
Ageneralizedexistencetheoremofbackwarddoublystochasticdifferentialequations[J].
ActaMathematicaSinica:EnglishSeries,2010,26(8):1525-1534.
[10]朱波,韩宝燕.
非Lipschitz条件下的倒向重随机微分方程[J].
数学物理学报,2008,28A(5):977-984.
[11]NaulartD,PardouxE.
Stochasticcalculuswithanticipatinginte-grands[J].
ProbabTheoryRelatFields,1988,78(4):535-581.
[12]马戈,堃黄.
半线性抛物方程各向异性有限元逼近[J].
江西师范大学学报:自然科学版,2010,34(5):480-483,494.
AClassofBDSDEswithUniformlyContinuousCoefficientsSONGLi1,2(1.
SchoolofFinance,ShandongLightIndustrySchool,Ji'nanShandong250100,China;2.
SchoolofMathematics,ShandongUniversity,Ji'nanShandong250100,China)Abstract:Bycomparisontheoremofbackwarddoublystochasticdifferentialequationsandapproximationoffunction,aclassofone-dimensionalbackwarddoublystochasticdifferentialequations(BDSDEs)isstudied,wherethecoefficientsisuniformlycontinuous.
AnexistencetheoremforsolutionsoftheclassofBDSDEsisobtained,whichgeneralizesthesituationthatthecoefficientsatisfyLipschitzconditions.
Keywords:backwarddoublystochasticdifferentialequation;backwardstochasticintegral;existencetheorem(责任编辑:曾剑锋)
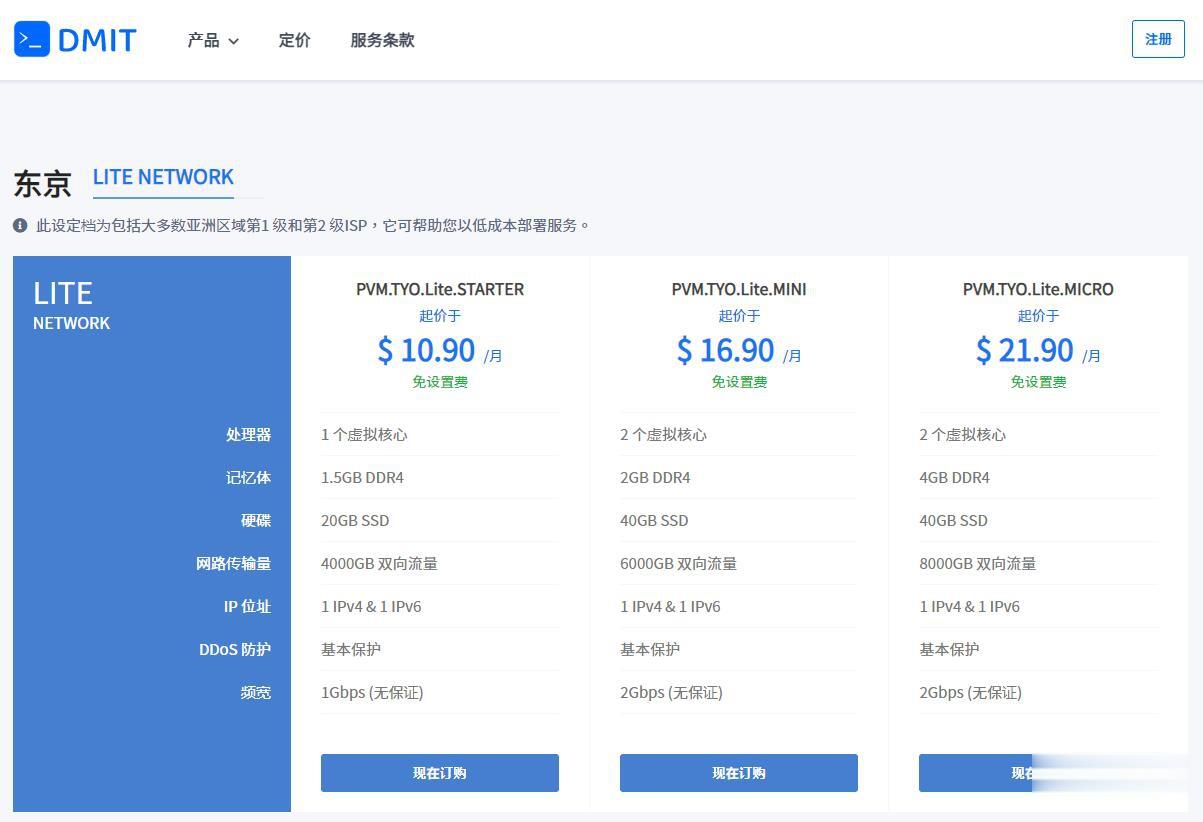
DMIT$10.9/月,日本VPS/三网直连/1核1.5G内存/20GB存储/1Gbps端口
优惠码年付一次性5折优惠码:TYO-Lite-Open-Beta-1y-50OFF永久8折优惠码:TYO-Lite-Open-Beta-Recur-20OFF日本vpsCPU内存SSD流量带宽价格购买1核1.5G20 GB4 TB1Gbps$10.9/月购买2核2 G40 GB6 TB1Gbps$16.9/月购买2核4 G60 GB8 TB1Gbps$21.9/月购买4核4 G80 GB12 TB...
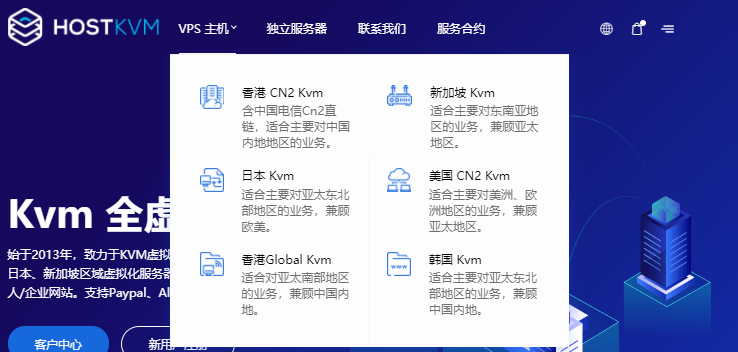
HostKvm新上联通CUVIP线路VPS,八折优惠后1G内存套餐$5.2/月起
最近上洛杉矶机房联通CUVIP线路主机的商家越来越多了,HostKvm也发来了新节点上线的邮件,适用全场8折优惠码,基于KVM架构,优惠后最低月付5.2美元起。HostKvm是一家成立于2013年的国人主机商,提供基于KVM架构的VPS主机,可选数据中心包括日本、新加坡、韩国、美国、中国香港等多个地区机房,君选择国内直连或优化线路,延迟较低,适合建站或者远程办公等。以洛杉矶CUVIP线路主机为例,...
特网云(198元/月),高质量云虚拟主机低至0.16元/天,裸金属服务器仅需10.5元/天
特网云为您提供高速、稳定、安全、弹性的云计算服务计算、存储、监控、安全,完善的云产品满足您的一切所需,深耕云计算领域10余年;我们拥有前沿的核心技术,始终致力于为政府机构、企业组织和个人开发者提供稳定、安全、可靠、高性价比的云计算产品与服务。官方网站:https://www.56dr.com/ 10年老品牌 值得信赖 有需要的请联系======================特网云推出多IP云主机...
唯一的结果为你推荐
-
投资者适当性客户端系统学生微信5支持ipad流量支付宝photoshop技术ps几大关键技术?ipad如何上网iPad怎么上网?请高手指点ipad连不上wifiiPad mini WiFi开关成灰色无法连接,怎么办iphone连不上wifi苹果手机无法连接wifi是什么原因phpechophp echo函数 是什么意思联通版iphone4s苹果4s怎么分移动版联通版电信版?