公式成龙演出遇小意外
成龙演出遇小意外 时间:2021-04-25 阅读:()
《逻辑与认知》电子期刊2004年第3期1一个极小的弗协调逻辑系统1余俊伟(中国人民大学哲学系,北京,100872)摘要:从Cω.
去掉双重否定律可得到一个比科斯塔弗协调逻辑系统Cω.
更小的系统.
它有一个克里普克语义解释;论文证明了该系统相对于该解释既是可靠的又是完全的.
关键词:弗协调逻辑;可靠性;完全性中图分类号:B81文献标识码:A弗协调逻辑开创者科斯塔建立了一系列弗协调逻辑系统Cn(1≤n≤ω),其中Cω为最小.
Cω是以直觉主义命题逻辑的正部分加上排中律和双重否定律得到的;北欧的D.
Batens以经典命题逻辑的正部分加上排中律得到了弱的弗协调逻辑CLuN,并以此为基础扩张得到了两个逻辑系统,它们都介于CLuN和经典逻辑之间.
系统经典命题逻辑的正部分与直觉主义逻辑的正部分相比多了皮尔士律.
笔者介绍的这个系统是以直觉主义命题逻辑的正部分仅加上排中律得到的.
比Cω和CLuN都小,推理能力是最弱的,但它也说明还有比已知两种否定更弱的否定.
(一)L语法:1、MPL建立在语言L之上,L由以下三类符号组成:第一类包括可数无穷多个命题符:p0,p1,p2,…,pm,…,m为自然数.
第二类包括四个联结词:,∧,∨,→.
第三类包括两个标点符号:(,);它们依次被称为左括号和右括号.
由初始符号组成的有穷序列称之为符号.
由全体符号形成的集合,我们将它记为Expr(L).
定义1L的一个公式是也仅是按下列规则构成的符号:(1)单独的命题符号是公式,(2)若α是公式,则α是公式,1本文得到国家社会科学基金项目(04CZX010)的资助.
《逻辑与认知》电子期刊2004年第3期2(3)若α,β是公式,则(α∧β),(α∨β),(α→β)是公式.
单独的命题符号是最简单的公式,被称为原子公式.
由全体原子公式所组成的符号集记为Atom(L),全体公式组成的符号集记为Form(L).
我们用α,β和γ等表示任意的公式.
显然,Form(L)将包含Atom(L).
定义2对L中的公式α、β(1)α中的联结词,∧,∨,→出现的总次数称为α的复杂度;(2)α作为β的一个连续部分出现,我们就称α是β的子公式;如果α是β的子公式且α不等于β,就称α是β的真子公式;(3)我们称只出现在α中而不出现在α的任何真子公式中的那个联结词为α的主联结词;我们称主联结词是的公式为否定式;主联结词是∧的公式为合取式;主联结词是∨的公式为析取式;主联结词是→的公式为蕴涵式.
(4)α中某个的辖域是指在α中紧随该出现的α的子公式;α中某个→的左辖域和右辖域是指在α中紧随该→出现的α的左、右两个子公式,对∧与∨的辖域定义类似.
MPL的公理模式有如下九条:(1)α→(β→α),(2)(α→(β→γ)→((α→β)→(α→γ)),(3)α→(β→α∧β),(4)α∧β→α,(5)α∧β→β,(6)(α→γ)→((β→γ)→(α∨β→γ)),(7)α→α∨β,(8)β→α∨β,(9)α∨α,MPL的推理规则:R(→消去规则):从α和α→β可推出β.
定义3MPL的形式可推演关系定义如下.
由公式集Г到α的一个推演是一个有穷公式序列α1,α2,…,αm,使得αm是α并且对于各个j(1≤j≤m),αj满足下列条件之一:(1)αj是MPL的公理,(2)αj∈Г,(3)有小于j的i和k使得αj可从αi和αk利用→消去规则而得到.
如果有一个由Г到α的推演,则称α在系统MPL中是由Г形式可推演的,记为ГMPLα,在不发生混淆的情况下简记为Гα.
否则,称α在系统MPL中不是由Г形式可推演的,记为Г/MPLα,在不发生混淆的情况下简记为Г/α.
当Г为空集时,我们称这个有穷序列《逻辑与认知》电子期刊2004年第3期3为α的一个证明,也称α在MPL中是可证的.
我们称一个可证的公式为MPL的一个定理.
若Г={α1,α2,…,αm},则Γα可记为α1,α2,…,αmα.
Γ∪{α}β可记为Γ,αβ.
若Γ为空集,Γα可记为α.
此时α是MPL的一个定理.
定理1MPL中有下列推演规则:(1)如果α∈Г,那么Γα,(2)如果Γ并且Γ,那么α,(3)如果Γα,Γα→β,那么Γβ.
定理2MPL有演绎定理.
对其成立(二)L语义:定义4一个L框架是一个有序二元组〈W,R〉,其中W是一非空集,R是W上的一偏序,即满足自返性和传递性.
定义5一个L模型是一个有序三元组〈W,R,V〉,其中〈W,R〉是一个L框架,V是从Form(L)*W到{1,0}中的一个映射,满足以下条件:(1)如果V(α,w)=0,那么,对任一w1∈W,若wRw1,则V(α,w)=1,(2)V(α∧β,w)=1当且仅当V(α,w)且V(β,w)=1,(3)V(α∨β,w)=1当且仅当V(α,w)=1或V(β,w)=1,(4)V(α→β,w)=1当且仅当对任一w1∈W,若wRw1,则V(α,w1)=0或V(β,w)=1,(5)对L的任意公式α,W中的任意两个元素w1,w2,如果w1Rw2且V(α,w1)=1,那么V(α,w2)=1.
称此模型为建立在框架〈W,R〉上的一个模型.
定义6令为一L框架,α为L的任一公式.
如果存在〈W,R〉上的一个模型和W中的一个元素w,使得V(α,w)=1,那么我们就称α是可满足的,可记为α,或简单记为wα,称是α的模型.
如果是公式集Γ中的任意公式α的模型,则称它是Γ的模型;如果对〈W,R〉上的任意一个模型,任意w∈W都有V(α,w)=1,就称α在框架上有效,记为α.
如果α在任意一个L框架上有效,则称α是L有效的,记为Lα,在不发生混淆的情况下简记为α.
否则,称α不是L有效的,记为/Lα.
定理3如果α,则α,即MPL相对于L框架具有可靠性.
证明:假设α.
于是存在一个有穷公式序列α1,α2,…,αm,使得αm是α并且对于各个j(1≤j≤m),αj满足下列条件之一:(1)αj是MPL的公理,(2)有小于j的i和k使得αj可从αi和αk利用→消去规则而得到.
我们施归纳于j(1≤j≤m)证明对每一j都有αj.
当j=1时.
αj是MPL的公理.
由下可得α是L有效的,因此αj.
《逻辑与认知》电子期刊2004年第3期4如果它属公理模式(1).
假设它不是L有效的,则存在一个L框架〈W,R〉,在它上有一模型〈W,R,V〉并且W中有一元素w使得V(α→(β→α),w)=0,则据定义5(4)存在一个W中的一个元素w1满足:wRw1并且V(α,w1)=1且V(β→α,w1)=0,则据定义5(4)存在一个W中的一个元素w2满足:w1Rw2并且V(β,w2)=1且V(α,w2)=0,但根据定义5(5)又有V(α,w2)=1.
这样就产生矛盾.
因此它是L有效的.
如果它属公理模式(2).
假设它不是L有效的,则存在一个L框架〈W,R〉,在它上有一模型〈W,R,V〉并且W中有一元素w使得V((α→(β→γ)→((α→β)→(α→γ)),w)=0,则据定义5(4)存在一个W中的一个元素w1满足:wRw1并且V(α→(β→γ),w1)=1且V((α→β)→(α→γ),w1)=0,则据定义5(4)存在一个W中的一个元素w2满足:w1Rw2并且V(α→β,w2)=1且V(α→γ,w2)=0,据定义5(4)存在一个W中的一个元素w3满足:w2Rw3并且V(α,w3)=1且V(γ,w3)=0.
但L框架具有传递性,因此,w1Rw3;又根据定义5(5)有V(α→(β→γ),w3)=1且V(α→β,w3)=1,与V(α,w3)=1根据定义5(4)和L框架具有自返性一起可以得到V(β,w3)=1和V(β→γ,w3)=1,进而V(γ,w3)=1.
这样就产生矛盾.
因此它是L有效的.
如果它属公理模式(3).
假设它不是L有效的,则存在一个L框架〈W,R〉,在它上有一模型〈W,R,V〉并且W中有一元素w使得V(α→(β→α∧β),w)=0,则据定义5(4)存在一个W中的一个元素w1满足:wRw1并且V(α,w1)=1且V(β→(α∧β),w1)=0,则据定义5(4)存在一个W中的一个元素w2满足:w1Rw2并且V(β,w2)=1且V(α∧β,w2)=0,但根据定义5(5)又有V(α,w2)=1.
这样就与定义5(2)产生矛盾.
因此它是L有效的.
如果它属公理模式(4).
假设它不是L有效的,则存在一个L框架〈W,R〉,在它上有一模型〈W,R,V〉并且W中有一元素w使得V(α∧β→α,w)=0,则据定义5(4)存在一个W中的一个元素w1满足:wRw1并且V(α∧β,w1)=1且V(α,w1)=0,与定义5(2)产生矛盾.
因此它是L有效的.
类似可证如果它属公理模式(5),也同样是L有效的.
如果它属公理模式(6).
假设它不是L有效的,则存在一个L框架〈W,R〉,在它上有一模型〈W,R,V〉并且W中有一元素w使得V((α→γ)→((β→γ)→(α∨β→γ)),w)=0,则据定义5(4)存在一个W中的一个元素w1满足:wRw1并且V(α→γ,w1)=1且V((β→γ)→(α∨β→γ),w1)=0,据定义5(4)存在一个W中的一个元素w2满足:w1Rw2并且V(β→γ,w2)=1且V((α∨β→γ,w2)=0,据定义5(4)存在一个W中的一个元素w3满足:w2Rw3并且V(α∨β,w3)=1且V(γ,w3)=0,但L框架具有传递性,因此,w1Rw3;又根据定义5(5)有V(α→γ,w3)=1与V(β→γ,w3)=1,V(β→γ,w3)=1与V(γ,w3)=0根据定义5(4)和L框架具有自返性一起得到V(β,w3)=0;同理可得V(α,w3)=0,因此根据定义5(3)有V(α∨β,w3)=0.
这与V(α∨β,w3)=1产生矛盾.
因此它是L有效的.
如果它属公理模式(7).
假设它不是L有效的,则存在一个L框架〈W,R〉,在它上有一模型〈W,R,V〉并且W中有一元素w使得V(α→α∨β,w)=0,则据定义5(4)存在一个W中的一个元素w1满足:wRw1并且V(α,w1)=1且V(α∨β,w1)=0,与定义5(3)矛盾.
因此它是L有效的.
类似可证如果它属公理模式(8),也同样是L有效的.
如果它属公理模式(9).
假设它不是L有效的,则存在一个L框架〈W,R〉,在它上有一模型〈W,R,V〉并且W中有一元素w使得V(α∨α,w)=0,则据定义5(3)《逻辑与认知》电子期刊2004年第3期5有V(α,w)=0且V(α,w)=0.
因为wRw,据定义5(1)由V(α,w)=0可得V(α,w)=1,这样就产生矛盾.
因此它是L有效的.
假设j=n时成立,当j=n+1时,如果αj是MPL的公理,如上已证得.
如果有小于j的i和k使得αj可从αi和αk利用→消去规则而得到,则由归纳假设已得αi和αk.
不妨设αk=αi→αj.
如果/αj,则存在一个L框架〈W,R〉,在它上有一模型〈W,R,V〉并且W中有一元素w使得V(αj,w)=0,但是αi和αi→αj是L有效的,因此V(αi,w)=1且V(αi→αj,w)=1,但L框架具有自返性,根据定义5(4)有V(αj,w)=1,与刚才假设的V(αj,w)=0矛盾.
所以有αj.
由上证明了:如果α,则α.
定义7一公式集Γ称为足道集,如果存在L公式α使得Γ/α.
如果足道集Γ对公式α有Γ/α,也称Γ是α-足道的.
定义8一公式集Γ称为极大足道集,如果它满足:(1)是足道集.
(2)对任一L公式α,如果Γα,则α∈Γ.
(3)对L公式α、β,若α∨β∈Γ,则有α∈Γ或β∈Γ.
引理1对任一α-足道的公式集都能扩张为一α-足道的极大足道集.
证明:设Γ是任一α-足道的.
我们现在来证明存在极大足道集满足:Γ并且/α.
因而,Γ扩张为一α-足道的极大足道集.
将L的所有形如α∨β的析取式排列如下:γ1,γ2,…,γn,….
下面构造公式集系列Γ1,Γ2,…,Γn,…,如下:令Γ1=Γ.
依次考察上述析取式排列中公式γ1,γ2,…,看是否可由Γ1推演出,设γi是上述析取式排列的第一个可以由Γ1推演出的公式,即Γ1γi,但对每一j,其中W={w|w是MPL的极大足道集},R={|w1,w2∈W,w1w2},V是从Form(L)*W到{1,0}中的一个映射,满足以下条件:V(α,w)=1当且仅当α∈w.
如果V(α,w)=0,那么αw,由引理2(1)得对任一满足条件ww1,也即wRw1《逻辑与认知》电子期刊2004年第3期7的极大足道集w1都有α∈w1,因此V(α,w1)=1.
V(α∧β,w)=1当且仅当α∧β∈w当且仅当α∈w且β∈w当且仅当V(α,w)且V(β,w)=1.
V(α∨β,w)=1当且仅当α∨β∈w当且仅当α∈w或β∈w当且仅当V(α,w)=1或V(β,w)=1.
V(α→β,w)=1当且仅当α→β∈w当且仅当对任一满足条件ww1,也即wRw1的极大足道集w1都有αw1或β∈w1,即V(α,w1)=0或V(β,w)=1,对L的任意公式α,W中的任意两个元素w1,w2,如果w1Rw2且V(α,w1)=1,那么据R定义和V的定义有w1w2且α∈w1,于是有α∈w2,因此V(α,w2)=1.
因此M为一L模型,由假设/α得则存在一极大足道集Γ/α.
因此Γ∈W,并且αΓ.
据M定义有V(α,Γ)=0.
因此/α.
参考文献:[1].
张清宇.
弗协调逻辑[M].
北京:中国社会出版社.
2003[2].
冯棉.
经典逻辑与直觉主义逻辑[M].
上海:上海人民出版社.
1989[3]张清宇,郭世铭,李小五.
哲学逻辑研究[M].
北京:社会科学文献出版社.
1997[4]刘壮虎.
逻辑演算[M].
北京:中国社会科学出版社.
1993[5]MaxUrchs.
RecentTrendsinParaconsistentLogic[A].
W.
Heinrich.
EssaysontheNon-ClassicalLogic[C].
WorldScientificPublishingCo.
Pte.
Ltd,2003.
[6]ArahamPriest,RichardRoutley,JeanNorman.
ParaconsistentLogic:EssaysontheInconsistent[C].
PhilosophiaVerlagGmbH,München.
,1989AMinimalParaconsistentLogicSystemYuJun-wei(PhilosophyDepartment,RenminUniversityofChina,Beijing,100872,China)Abstract:WegetaweakerparaconsistentlogicsystemMPLthanCω.
bydleting(removing)α→αfromCω.
We.
giveaKripklesemanticsandprovethatMPLissoundandcompletewithrespecttothesemantics.
Keywords:paraconsistentlogic;sound;complete收稿日期:2004-06-01;基金项目:国家社会科学基金项目《弗协调相干道义逻辑研究》(04CZX010).
作者简介:余俊伟,1974年生,男,汉族,江西安义人,中国人民大学副教授.
去掉双重否定律可得到一个比科斯塔弗协调逻辑系统Cω.
更小的系统.
它有一个克里普克语义解释;论文证明了该系统相对于该解释既是可靠的又是完全的.
关键词:弗协调逻辑;可靠性;完全性中图分类号:B81文献标识码:A弗协调逻辑开创者科斯塔建立了一系列弗协调逻辑系统Cn(1≤n≤ω),其中Cω为最小.
Cω是以直觉主义命题逻辑的正部分加上排中律和双重否定律得到的;北欧的D.
Batens以经典命题逻辑的正部分加上排中律得到了弱的弗协调逻辑CLuN,并以此为基础扩张得到了两个逻辑系统,它们都介于CLuN和经典逻辑之间.
系统经典命题逻辑的正部分与直觉主义逻辑的正部分相比多了皮尔士律.
笔者介绍的这个系统是以直觉主义命题逻辑的正部分仅加上排中律得到的.
比Cω和CLuN都小,推理能力是最弱的,但它也说明还有比已知两种否定更弱的否定.
(一)L语法:1、MPL建立在语言L之上,L由以下三类符号组成:第一类包括可数无穷多个命题符:p0,p1,p2,…,pm,…,m为自然数.
第二类包括四个联结词:,∧,∨,→.
第三类包括两个标点符号:(,);它们依次被称为左括号和右括号.
由初始符号组成的有穷序列称之为符号.
由全体符号形成的集合,我们将它记为Expr(L).
定义1L的一个公式是也仅是按下列规则构成的符号:(1)单独的命题符号是公式,(2)若α是公式,则α是公式,1本文得到国家社会科学基金项目(04CZX010)的资助.
《逻辑与认知》电子期刊2004年第3期2(3)若α,β是公式,则(α∧β),(α∨β),(α→β)是公式.
单独的命题符号是最简单的公式,被称为原子公式.
由全体原子公式所组成的符号集记为Atom(L),全体公式组成的符号集记为Form(L).
我们用α,β和γ等表示任意的公式.
显然,Form(L)将包含Atom(L).
定义2对L中的公式α、β(1)α中的联结词,∧,∨,→出现的总次数称为α的复杂度;(2)α作为β的一个连续部分出现,我们就称α是β的子公式;如果α是β的子公式且α不等于β,就称α是β的真子公式;(3)我们称只出现在α中而不出现在α的任何真子公式中的那个联结词为α的主联结词;我们称主联结词是的公式为否定式;主联结词是∧的公式为合取式;主联结词是∨的公式为析取式;主联结词是→的公式为蕴涵式.
(4)α中某个的辖域是指在α中紧随该出现的α的子公式;α中某个→的左辖域和右辖域是指在α中紧随该→出现的α的左、右两个子公式,对∧与∨的辖域定义类似.
MPL的公理模式有如下九条:(1)α→(β→α),(2)(α→(β→γ)→((α→β)→(α→γ)),(3)α→(β→α∧β),(4)α∧β→α,(5)α∧β→β,(6)(α→γ)→((β→γ)→(α∨β→γ)),(7)α→α∨β,(8)β→α∨β,(9)α∨α,MPL的推理规则:R(→消去规则):从α和α→β可推出β.
定义3MPL的形式可推演关系定义如下.
由公式集Г到α的一个推演是一个有穷公式序列α1,α2,…,αm,使得αm是α并且对于各个j(1≤j≤m),αj满足下列条件之一:(1)αj是MPL的公理,(2)αj∈Г,(3)有小于j的i和k使得αj可从αi和αk利用→消去规则而得到.
如果有一个由Г到α的推演,则称α在系统MPL中是由Г形式可推演的,记为ГMPLα,在不发生混淆的情况下简记为Гα.
否则,称α在系统MPL中不是由Г形式可推演的,记为Г/MPLα,在不发生混淆的情况下简记为Г/α.
当Г为空集时,我们称这个有穷序列《逻辑与认知》电子期刊2004年第3期3为α的一个证明,也称α在MPL中是可证的.
我们称一个可证的公式为MPL的一个定理.
若Г={α1,α2,…,αm},则Γα可记为α1,α2,…,αmα.
Γ∪{α}β可记为Γ,αβ.
若Γ为空集,Γα可记为α.
此时α是MPL的一个定理.
定理1MPL中有下列推演规则:(1)如果α∈Г,那么Γα,(2)如果Γ并且Γ,那么α,(3)如果Γα,Γα→β,那么Γβ.
定理2MPL有演绎定理.
对其成立(二)L语义:定义4一个L框架是一个有序二元组〈W,R〉,其中W是一非空集,R是W上的一偏序,即满足自返性和传递性.
定义5一个L模型是一个有序三元组〈W,R,V〉,其中〈W,R〉是一个L框架,V是从Form(L)*W到{1,0}中的一个映射,满足以下条件:(1)如果V(α,w)=0,那么,对任一w1∈W,若wRw1,则V(α,w)=1,(2)V(α∧β,w)=1当且仅当V(α,w)且V(β,w)=1,(3)V(α∨β,w)=1当且仅当V(α,w)=1或V(β,w)=1,(4)V(α→β,w)=1当且仅当对任一w1∈W,若wRw1,则V(α,w1)=0或V(β,w)=1,(5)对L的任意公式α,W中的任意两个元素w1,w2,如果w1Rw2且V(α,w1)=1,那么V(α,w2)=1.
称此模型为建立在框架〈W,R〉上的一个模型.
定义6令为一L框架,α为L的任一公式.
如果存在〈W,R〉上的一个模型和W中的一个元素w,使得V(α,w)=1,那么我们就称α是可满足的,可记为α,或简单记为wα,称是α的模型.
如果是公式集Γ中的任意公式α的模型,则称它是Γ的模型;如果对〈W,R〉上的任意一个模型,任意w∈W都有V(α,w)=1,就称α在框架上有效,记为α.
如果α在任意一个L框架上有效,则称α是L有效的,记为Lα,在不发生混淆的情况下简记为α.
否则,称α不是L有效的,记为/Lα.
定理3如果α,则α,即MPL相对于L框架具有可靠性.
证明:假设α.
于是存在一个有穷公式序列α1,α2,…,αm,使得αm是α并且对于各个j(1≤j≤m),αj满足下列条件之一:(1)αj是MPL的公理,(2)有小于j的i和k使得αj可从αi和αk利用→消去规则而得到.
我们施归纳于j(1≤j≤m)证明对每一j都有αj.
当j=1时.
αj是MPL的公理.
由下可得α是L有效的,因此αj.
《逻辑与认知》电子期刊2004年第3期4如果它属公理模式(1).
假设它不是L有效的,则存在一个L框架〈W,R〉,在它上有一模型〈W,R,V〉并且W中有一元素w使得V(α→(β→α),w)=0,则据定义5(4)存在一个W中的一个元素w1满足:wRw1并且V(α,w1)=1且V(β→α,w1)=0,则据定义5(4)存在一个W中的一个元素w2满足:w1Rw2并且V(β,w2)=1且V(α,w2)=0,但根据定义5(5)又有V(α,w2)=1.
这样就产生矛盾.
因此它是L有效的.
如果它属公理模式(2).
假设它不是L有效的,则存在一个L框架〈W,R〉,在它上有一模型〈W,R,V〉并且W中有一元素w使得V((α→(β→γ)→((α→β)→(α→γ)),w)=0,则据定义5(4)存在一个W中的一个元素w1满足:wRw1并且V(α→(β→γ),w1)=1且V((α→β)→(α→γ),w1)=0,则据定义5(4)存在一个W中的一个元素w2满足:w1Rw2并且V(α→β,w2)=1且V(α→γ,w2)=0,据定义5(4)存在一个W中的一个元素w3满足:w2Rw3并且V(α,w3)=1且V(γ,w3)=0.
但L框架具有传递性,因此,w1Rw3;又根据定义5(5)有V(α→(β→γ),w3)=1且V(α→β,w3)=1,与V(α,w3)=1根据定义5(4)和L框架具有自返性一起可以得到V(β,w3)=1和V(β→γ,w3)=1,进而V(γ,w3)=1.
这样就产生矛盾.
因此它是L有效的.
如果它属公理模式(3).
假设它不是L有效的,则存在一个L框架〈W,R〉,在它上有一模型〈W,R,V〉并且W中有一元素w使得V(α→(β→α∧β),w)=0,则据定义5(4)存在一个W中的一个元素w1满足:wRw1并且V(α,w1)=1且V(β→(α∧β),w1)=0,则据定义5(4)存在一个W中的一个元素w2满足:w1Rw2并且V(β,w2)=1且V(α∧β,w2)=0,但根据定义5(5)又有V(α,w2)=1.
这样就与定义5(2)产生矛盾.
因此它是L有效的.
如果它属公理模式(4).
假设它不是L有效的,则存在一个L框架〈W,R〉,在它上有一模型〈W,R,V〉并且W中有一元素w使得V(α∧β→α,w)=0,则据定义5(4)存在一个W中的一个元素w1满足:wRw1并且V(α∧β,w1)=1且V(α,w1)=0,与定义5(2)产生矛盾.
因此它是L有效的.
类似可证如果它属公理模式(5),也同样是L有效的.
如果它属公理模式(6).
假设它不是L有效的,则存在一个L框架〈W,R〉,在它上有一模型〈W,R,V〉并且W中有一元素w使得V((α→γ)→((β→γ)→(α∨β→γ)),w)=0,则据定义5(4)存在一个W中的一个元素w1满足:wRw1并且V(α→γ,w1)=1且V((β→γ)→(α∨β→γ),w1)=0,据定义5(4)存在一个W中的一个元素w2满足:w1Rw2并且V(β→γ,w2)=1且V((α∨β→γ,w2)=0,据定义5(4)存在一个W中的一个元素w3满足:w2Rw3并且V(α∨β,w3)=1且V(γ,w3)=0,但L框架具有传递性,因此,w1Rw3;又根据定义5(5)有V(α→γ,w3)=1与V(β→γ,w3)=1,V(β→γ,w3)=1与V(γ,w3)=0根据定义5(4)和L框架具有自返性一起得到V(β,w3)=0;同理可得V(α,w3)=0,因此根据定义5(3)有V(α∨β,w3)=0.
这与V(α∨β,w3)=1产生矛盾.
因此它是L有效的.
如果它属公理模式(7).
假设它不是L有效的,则存在一个L框架〈W,R〉,在它上有一模型〈W,R,V〉并且W中有一元素w使得V(α→α∨β,w)=0,则据定义5(4)存在一个W中的一个元素w1满足:wRw1并且V(α,w1)=1且V(α∨β,w1)=0,与定义5(3)矛盾.
因此它是L有效的.
类似可证如果它属公理模式(8),也同样是L有效的.
如果它属公理模式(9).
假设它不是L有效的,则存在一个L框架〈W,R〉,在它上有一模型〈W,R,V〉并且W中有一元素w使得V(α∨α,w)=0,则据定义5(3)《逻辑与认知》电子期刊2004年第3期5有V(α,w)=0且V(α,w)=0.
因为wRw,据定义5(1)由V(α,w)=0可得V(α,w)=1,这样就产生矛盾.
因此它是L有效的.
假设j=n时成立,当j=n+1时,如果αj是MPL的公理,如上已证得.
如果有小于j的i和k使得αj可从αi和αk利用→消去规则而得到,则由归纳假设已得αi和αk.
不妨设αk=αi→αj.
如果/αj,则存在一个L框架〈W,R〉,在它上有一模型〈W,R,V〉并且W中有一元素w使得V(αj,w)=0,但是αi和αi→αj是L有效的,因此V(αi,w)=1且V(αi→αj,w)=1,但L框架具有自返性,根据定义5(4)有V(αj,w)=1,与刚才假设的V(αj,w)=0矛盾.
所以有αj.
由上证明了:如果α,则α.
定义7一公式集Γ称为足道集,如果存在L公式α使得Γ/α.
如果足道集Γ对公式α有Γ/α,也称Γ是α-足道的.
定义8一公式集Γ称为极大足道集,如果它满足:(1)是足道集.
(2)对任一L公式α,如果Γα,则α∈Γ.
(3)对L公式α、β,若α∨β∈Γ,则有α∈Γ或β∈Γ.
引理1对任一α-足道的公式集都能扩张为一α-足道的极大足道集.
证明:设Γ是任一α-足道的.
我们现在来证明存在极大足道集满足:Γ并且/α.
因而,Γ扩张为一α-足道的极大足道集.
将L的所有形如α∨β的析取式排列如下:γ1,γ2,…,γn,….
下面构造公式集系列Γ1,Γ2,…,Γn,…,如下:令Γ1=Γ.
依次考察上述析取式排列中公式γ1,γ2,…,看是否可由Γ1推演出,设γi是上述析取式排列的第一个可以由Γ1推演出的公式,即Γ1γi,但对每一j,其中W={w|w是MPL的极大足道集},R={|w1,w2∈W,w1w2},V是从Form(L)*W到{1,0}中的一个映射,满足以下条件:V(α,w)=1当且仅当α∈w.
如果V(α,w)=0,那么αw,由引理2(1)得对任一满足条件ww1,也即wRw1《逻辑与认知》电子期刊2004年第3期7的极大足道集w1都有α∈w1,因此V(α,w1)=1.
V(α∧β,w)=1当且仅当α∧β∈w当且仅当α∈w且β∈w当且仅当V(α,w)且V(β,w)=1.
V(α∨β,w)=1当且仅当α∨β∈w当且仅当α∈w或β∈w当且仅当V(α,w)=1或V(β,w)=1.
V(α→β,w)=1当且仅当α→β∈w当且仅当对任一满足条件ww1,也即wRw1的极大足道集w1都有αw1或β∈w1,即V(α,w1)=0或V(β,w)=1,对L的任意公式α,W中的任意两个元素w1,w2,如果w1Rw2且V(α,w1)=1,那么据R定义和V的定义有w1w2且α∈w1,于是有α∈w2,因此V(α,w2)=1.
因此M为一L模型,由假设/α得则存在一极大足道集Γ/α.
因此Γ∈W,并且αΓ.
据M定义有V(α,Γ)=0.
因此/α.
参考文献:[1].
张清宇.
弗协调逻辑[M].
北京:中国社会出版社.
2003[2].
冯棉.
经典逻辑与直觉主义逻辑[M].
上海:上海人民出版社.
1989[3]张清宇,郭世铭,李小五.
哲学逻辑研究[M].
北京:社会科学文献出版社.
1997[4]刘壮虎.
逻辑演算[M].
北京:中国社会科学出版社.
1993[5]MaxUrchs.
RecentTrendsinParaconsistentLogic[A].
W.
Heinrich.
EssaysontheNon-ClassicalLogic[C].
WorldScientificPublishingCo.
Pte.
Ltd,2003.
[6]ArahamPriest,RichardRoutley,JeanNorman.
ParaconsistentLogic:EssaysontheInconsistent[C].
PhilosophiaVerlagGmbH,München.
,1989AMinimalParaconsistentLogicSystemYuJun-wei(PhilosophyDepartment,RenminUniversityofChina,Beijing,100872,China)Abstract:WegetaweakerparaconsistentlogicsystemMPLthanCω.
bydleting(removing)α→αfromCω.
We.
giveaKripklesemanticsandprovethatMPLissoundandcompletewithrespecttothesemantics.
Keywords:paraconsistentlogic;sound;complete收稿日期:2004-06-01;基金项目:国家社会科学基金项目《弗协调相干道义逻辑研究》(04CZX010).
作者简介:余俊伟,1974年生,男,汉族,江西安义人,中国人民大学副教授.
- 公式成龙演出遇小意外相关文档
- 湖人成龙演出遇小意外
- 2020年北京高考名著阅读《红楼梦》重点解析
- 2018年"茶香中国"首届全国采茶戏汇演精品小戏折子戏交流演出安排表
- 二二成龙演出遇小意外
- 四川省成都市群众信访举报转办和边督边改公开情况一览表
- 朔州市成龙演出遇小意外
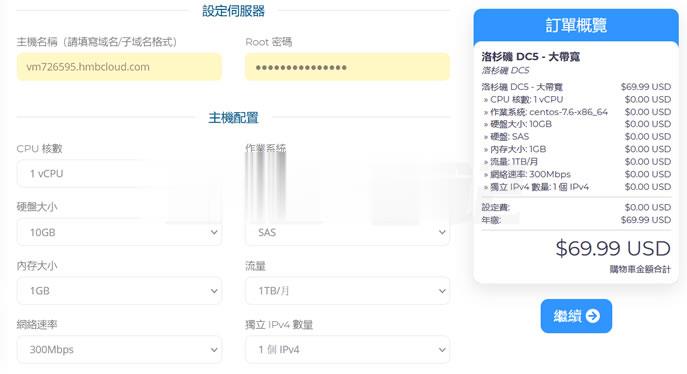
半月湾hmbcloud升级500Mbps带宽,原生VPS,$4.99/月
关于半月湾HMBCloud商家之前也有几篇那文章介绍过这个商家的产品,对于他们家的其他产品我都没有多加留意,而是对他们家的DC5机房很多人还是比较喜欢的,这个比我们有些比较熟悉的某商家DC6 DC9机房限时,而且半月湾HMBCloud商家是相对便宜的。关于半月湾DC5机房的方案选择和介绍:1、半月湾三网洛杉矶DC5 CN2 GIA同款DC6 DC9 1G内存 1TB流量 月$4.992、亲测选择半...
Friendhosting 黑色星期五 VDS/VPS可享四五折优惠促销
Friendhosting商家在前面的篇幅中也又陆续介绍到,是一家保加利亚主机商,主要提供销售VPS和独立服务器出租业务,数据中心分布在:荷兰、保加利亚、立陶宛、捷克、乌克兰和美国洛杉矶等。这不近期黑色星期五活动,商家也有推出了黑五优惠,VPS全场一次性45折,虚拟主机4折,全球多机房可选,老用户续费可获9折加送1个月使用时长,VDS折后最低仅€14.53/年,有需要的可以看看。Friendhos...
SugarHosts糖果主机,(67元/年)云服务器/虚拟主机低至半价
SugarHosts 糖果主机商也算是比较老牌的主机商,从2009年开始推出虚拟主机以来,目前当然还是以虚拟主机为主,也有新增云服务器和独立服务器。早年很多网友也比较争议他们家是不是国人商家,其实这些不是特别重要,我们很多国人商家或者国外商家主要还是看重的是品质和服务。一晃十二年过去,有看到SugarHosts糖果主机商12周年的促销活动。如果我们有需要香港、美国、德国虚拟主机的可以选择,他们家的...

成龙演出遇小意外为你推荐
-
现有新的ios更新可用请从ios14be苹果x更新系统14不能玩王者荣耀了有没有一样的?access数据库修复求救,ACCESS数据库破坏了,怎么修复?特朗普吐槽iPhone为什么iphone x卖的这么好字节跳动回应TikTok易主#北京字节跳动科技有限公司#小说审核有三面么?我面试了两轮就叫我回家等消息了 要是刷下来了也该告netshwinsockreset游戏出现battlEye Launcher 怎么办腾讯官方电话腾讯公司电话多少123456hd手机卡上出现符号hd怎么取消独立访客访客数(UV)是什么意思无忧登陆无忧登陆这个软件有毒吗shopex模板SHOPEX模板 修改整体宽度