byvoidjs中有哪些全局方法?
byvoid 时间:2021-07-10 阅读:()
BAT前端应届生的薪资大概有多少
我毕业的时候(08年) 腾讯7k 百度9k,麦克尔索芙特也就13k(貌似阿里当时更低完全没入眼) 今年出去面试,听完工资范围面试官都嫉妒得无心招聘了…… 话说阿里的实习生分 Ali star(比如之前很火的byvoid小朋友面试记录泄漏),A+,A,B+四档,一般入目。Pascal 的tarjan算法
强连通分量 一个有向图中,如果节点i能够通过一些边到达节点j,就 简写成i能到达j。如果对于任意两个节点i,j均有i能到达j或j能到达i,则说此图是连通的。
如果对于任意两个节点i,j均有i能到达j且j能到达i, 则说此图是强连通的。
对于一个无向图,说强联通没有意义,因为此时强连通就是连通。
而对于一个有向图,它不一定是强连通的,但可以分为几个极大的 强连通子图(“极大”的意思是再加入任何一个顶点就不满足强连通了)。
这些子图叫做这个有向图的强连通分量。
在上图中,强连通分量是 A{1},B{2,4},C{3,5,6,7}。
在一个强连通分量中的节点由于有着相似的拓扑性质,所以我们可以将其紧缩为一个节点(这让我想到了什么?化 学里的“族”),于是就大大减小了图的规模。
比如上图紧缩为A,B,C三个节点后,整个图就成为了B←A→C的简单形式。
所以强连通分量是一个 很有意义的东西。
然而如果根据定义,对每个节点进行一次O(n2)的DFS以求出它所能到达的顶点的话,整 个算法的时间复杂度就是迟钝的O(n3)。
下面将介绍用O(n2)求强连通分量的算 法:Tarjan算法。
Tarjan算法 Tarjan算法只要一遍DFS,效率高于Kosaraju。
它在技术上有了很大改进。
它基于的思想是:强连通分量是 DFS树中的子树(无论你如何进行DFS)。
Tarjan算法的过程是: ①在DFS树中,设low[x]是x或x的后代能够达到的最高的 祖先。
初始化时low[x]设为x。
②进行DFS,在结束节点x时计算low[x]。
计算的方法是:找出x能够到达的所有节点i,应保证 low[i]是x的祖先,即low[i]是灰点。
low[x]=highest(low[i]),即d[low[i]]最小。
③若 low[x]=x,则以x为根的子树就是一个强连通分量,输出并将其从树中删去。
我们依次得出: low[4]=low[2]=2 low[2]=low[4]=2 //{4,2}为强 连通分量 low[5]=low[3]=3 low[7]=low[5]=3 low[6]=low[7]=3 low[3]=low[6]=3 //{5,7,6,3}为强连通分量 low[1]=1 //{1}为强连通分量 程 序: var a,kl:array[1..1000,1..1000]of longint; d,f,low,stack:array[1..1000]of longint; i,j,n,time,h:longint; procedure dfs(x:longint); var i:longint; begin inc(time); d[x]:=time; inc(h); stack[h]:=x; for i:=1 to n do if a[x,i]>0 then begin if d[i]=0 then begin kl[x,i]:=1; dfs(i); end; if (d[i]>0)and(f[i]=0) then kl[x,i]:=2; if f[i]>0 then begin if d[x]>d[i] then kl[x,i]:=3 else kl[x,i]:=4; end; end; inc(time); f[x]:=time; for i:=1 to n do if a[x,i]>0 then if (f[low[i]]=0)and(d[low[i]]<d[low[x]])and(d[low[i]]>0) then low[x]:=low[i]; if low[x]=x then begin while stack[h]<>x do begin write(stack[h],); dec(h); end; writeln(stack[h]); dec(h); end; end; begin readln(n); for i:=1 to n do begin for j:=1 to n do read(a[i,j]); readln; end; fillchar(d,sizeof(d),0); fillchar(d,sizeof(d),0); for i:=1 to n do low[i]:=i; time:=0; fillchar(stack,sizeof(stack),0); h:=0; for i:=1 to n do if d[i]=0 then dfs(i); end. 还有,在BYVoid神牛的Blog里也讲到了Tarjan算法(图文并茂啊。
。
我就是看这个学的)。
js中有哪些全局方法?
类: Array, Boolean Date Error Number Object RegExp String 这些类有自己的方法, 生成对象后就可以用 方法: decodeURI decodeURIComponent encodeURI encodeURIComponent eval isFinite isNaN parseFloat parseInt
- byvoidjs中有哪些全局方法?相关文档
- byvoidC++编译时出错
- byvoid有关c语言void的问题,来大神啊,求解下面一段是什么意思
Hostinger 限时外贸美国主机活动 低至月12元且赠送1个COM域名
Hostinger 商家我们可能一些新用户不是太熟悉,因为我们很多新人用户都可能较多的直接从云服务器、独立服务器起步的。而Hostinger商家已经有将近十年的历史的商家,曾经主做低价虚拟主机,也是比较有知名度的,那时候也有接触过,不过一直没有过多的使用。这不这么多年过去,Hostinger商家一直比较稳妥的在运营,最近看到这个商家在改版UI后且产品上也在活动策划比较多。目前Hostinger在进...

€4.99/月Contabo云服务器,美国高性价比VPS/4核8G内存200G SSD存储
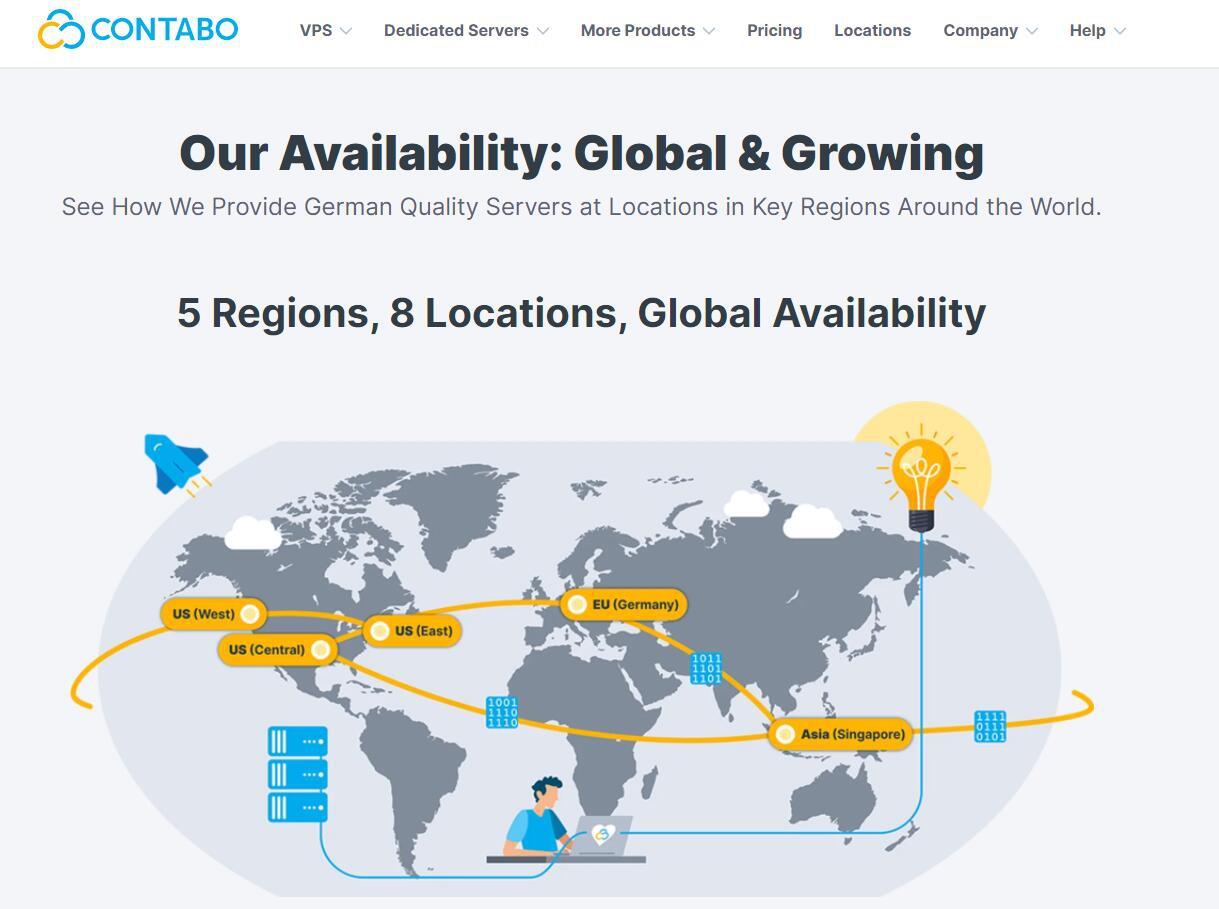
Contabo是一家运营了20多年的欧洲老牌主机商,之前主要是运营德国数据中心,Contabo在今年4月份增设新加坡数据中心,近期同时新增了美国纽约和西雅图数据中心。全球布局基本完成,目前可选的数据中心包括:德国本土、美国东部(纽约)、美国西部(西雅图)、美国中部(圣路易斯)和亚洲的新加坡数据中心。Contabo的之前国外主机测评网站有多次介绍,他们家的特点就是性价比高,而且这个高不是一般的高,是...
cyun29元/月,香港CN2 GIA云服务器低至起;香港多ip站群云服务器4核4G
cyun怎么样?cyun蓝米数据是一家(香港)藍米數據有限公司旗下品牌,蓝米云、蓝米主机等同属于该公司品牌。CYUN全系列云产品采用KVM架构,SSD磁盘阵列,优化线路,低延迟,高稳定。目前,cyun推出的香港云服务器性价比超高,香港cn2 gia云服务器,1核1G1M/系统盘+20G数据盘,低至29元/月起;香港多ip站群云服务器,16个ip/4核4G仅220元/月起,希望买香港站群服务器的站长...

byvoid为你推荐
-
sdfSDF文件怎么打开啊,或者用什么软件或程序打开xclient学校网络用的是H3C客户端,可不可以用xclient客户端替换onboardon board是什么意思?建站abc怎么取消技术支持: 建站ABC元宝网元宝网里面的一个币是真的投资赚钱吗oncontextmenu鼠标右键很好用,但是左键一点反应也没有,请问是什么原因呢?云图片云相册是什么意思郭凡生馬云的簡介3Q51信用卡论坛51信用卡贷了1200 现在还不上怎么办数据分析报告范文如何写数据分析报告?