函数2019高考数学二轮复习第一篇微型专题微专题02函数的图象与函数的应用练习理20190313296(数理化网)
02 函数的图象与函数的应用
1
∴y=.
答案▶ A
2.函数f(x)=log2x零点所在的区间为( ) .
A. 0
C. (1,2) D. (2,3)
解析▶ 函数f(x)的定义域为(0, +∞) ,且函数f(x)在(0, +∞)上为增函数.∵f,f(1)=log21,f(2)=log22f(3)=log23
∴f(1) ·f(2)<0,
∴函数f(x)=log2x.
答案▶ C
3.已知函数f(x)=的取值范围是( ) .
A. [-1,0) B. (1,2]
C. (1, +∞) D. (2, +∞)
解析▶ 当x≤2时,由-x2+4x=0,得x=0;
当x>2时,令f(x)=l og2x-a=0,得x=2a.
又函数f(x)有两个不同的零点,
∴2a>2,解得a>1,故选C.
答案▶ C
4.某企业为节能减排,用9万元购进一台新设备用于生产,第一年需运营费用2万元,从第二年起,每年运营费用均比上一年增加3万元,该设备每年生产的收入均为21万元,设该设备使用了n(n∈N*)年后,盈利总额达到最大值(盈利额等于收入减去成本) ,则n等于( ) .
A.6 B.7
C.8 D.7或8
解析▶ 盈利总额为21n-9-2+
由于对称轴为直线n=461,所以当n=7时,盈利总额取最大值,故选B.
答案▶ B
【例1】 函数y=sin x+ln|x|在区间[-3,3]上的图象大致为( ) .
解析▶ 设f(x)=sin x+ln|x|,
当x>0时
当x∈(0, 1)时,f' (x)>0,即函数f(x)在(0, 1)上为单调递增函数,排除B;
当x=1时,f(1)=sin 1>0,排除D;
因为f(-x)=sin(-x)+ln|-x|=-sinx+ln|x|,所以f(-x)≠±f(x) ,所以函数f(x)为非奇非偶函数,排除C.故选A.
答案▶ A
【例2】 函数y=sin x(1+cos 2x)在区间[-2,2]上的图象大致为( ) .
解析▶ 函数y=sin x(1+cos 2x)的定义域为[-2,2] ,其关于原点对称,且f(-x)=sin(-x) (1+cos 2x)=-sin x(1+cos 2x)=-f(x) ,则f(x)为奇函数,其图象关于原点对称,排除D;
当0<x<1时,y=sin x(1+cos 2x)=2sin xcos2x>0,排除C;
又2sin xcos.
答案▶ B
函数图象的辨识主要从以下几个方面入手: (1)函数图象的对称性; (2)函数图象的单调性; (3)特殊点.
1.函数f(x)=的图象大致是( ) .
解析▶ 当x≥0时,f(x)=2x-1,根据指数函数g(x)=2x的图象向下平移一个单位,即可得到函数f(x)的图象.
当x<0时,f(x)=-x2-2x,根据二次函数的图象与性质,可得到相应的图象.
综上,函数f(x)的图象为选项D中的图象.
答案▶ D
2.函数f(x)图象大致是( ) .
解析▶ 因为f(-x)其图象不关于y轴对称,所以可排除B,C.代入x=2,得f(x)<0,可排除A.故选D.
答案▶ D
【例3】 已知函数f(x)满足f(x+1)=f(x-1) ,且f(x)是偶函数,当x∈[-1,0]时,f(x)=x2,若在区间[-1,3]内,函数g(x)=f(x)-loga (x+2)有4个零点,则实数a的取值范围是( ) .
A. (1,5) B. (1,5]
C. (5, +∞) D. [5, +∞)
解析▶ 由题意可知函数f(x)是周期为2的偶函数,结合当x∈[-1,0]时,f(x)=x2,绘制函数图象如图所示,
函数g(x)有4个零点,则函数f(x)与函数y=l o ga (x+2)的图象在区间[-1,3]内有4个交点,结合函数图象可得, loga (3+2)≤1,解得a≥5,即实数a的取值范围是[5, +∞) .
答案▶ D
【例4】 定义在R上的奇函数f(x) ,当x≥0时,f(x)=的函数F(x)=f(x)-a(0<a<1)的所有零点之和为( ) .
A.2a-1 B. 1-2-a
C.-log2 (1+a) D. log2 (1-a)
解析▶ 当x≥0时,f(x)=
又f(x)是奇函数,画出函数f(x)的图象,
由函数f(x)图象和F(x)=0⇒f(x)=a(0<a<1) ,可知F(x)有五个零点,其中有两个零点关于直线x=-3对称,还有两个零点关于直线x=3对称,所以这四个零点的和为零,第五个零点是直线x=a与函数y=,故选C.
答案▶ C
函数零点的求解与判断方法: (1)直接求零点:令f(x)=0,如果能求出解,那么有几个解就有几个零点. (2)零点存在性定理:利用定理不仅要函数f(x)在区间[a,b]上的图象是连续不断的一条曲线,且f(a) ·f(b)<0,还必须结合函数的图象与性质(如单调性、奇偶性)才能确定函数有多少个零点. (3)利用图象交点的个数:将函数变形为两个函数的差,画出这两个函数的图象,看其交点的横坐标有几个不同的值,就有几个不同的零点.
1.定义在R上的偶函数f(x)满足f(x+1)=-f(x) ,当x∈[0, 1]时,f(x)=-2x+1,设函数g(x)=的图象所有交点的横坐标之和为( ) .
A.2 B.4 C.6 D.8
解析▶ 因为f(x+1)=-f(x)对称,作图可得四个交点的横坐标关于直线x=1对称,其和为2×2=4,故选B.
答案▶ B
2.函数f(x)=的取值范围是( ) .
A. [0, +∞) B. [0, 1]
C. (-1,0] D. [-1, +∞)
解析▶ 设t=f(x) ,则a=f(t) ,在同一坐标系内作y=a与y=f(t)的图象(如图) ,
当a≥-1时,两个图象有两个交点,设交点的横坐标分别为t1, t2,且t1<-1, t2≥-1.
当t1<-1时, t1=f(x)有一个解;当t2≥-1时, t2=f(x)有两个解.
综上可知,当a≥-1时,g(x)=f(f(x) )-a有三个不同的零点.故选D.
答案▶ D
【例5】 某高校为提升科研能力,计划逐年加大科研经费投入.若该高校2017年全年投入科研经费1300万元,在此基础上,每年投入的科研经费比上一年增长12%,则该高校全年投入的科研经费开始超过2000万元的年份是( ) . (参考数据: lg 1. 12≈0.05, lg
1.3≈0. 11, lg 2≈0.30)
A.2020年 B.2021年
C.2022年 D.2023年
解析▶ 若2018年是第1年,则第n年科研经费为1300×1. 12n.由1300×1. 12n>2000,可得lg 1.3+nlg 1. 12>lg 2,得n×0.05>0. 19,n>3.8,n≥4,即4年后,到2021年科研经费超过2000万元,故选B.
答案▶ B
与实际应用相结合的问题题型是高考命题的一个方向,解决此类问题的一般程序:.
在标准状况下,人体血液中氢离子的物质的量浓度(单位:mol/L,记作c(H+) )和氢氧根离子的物质的量浓度(单位:mol/L,记作c(OH-) )的乘积等于常数10-14.已知pH的定义为pH=-lgc(H+) ,健康人体血液的pH保持在7.35可以为( ) . (参考数据: lg 2≈0.30, lg 3≈0.48)
A.
解析▶ ∵cH(+) · cO H(-)=10-14,
∴.
∵7.35<-lgc(H+)<7.45,
∴10-7 45<c(H+)<10-7 35,
∴10
∵0.7>lg 3>lg 2.
答案▶ C
一、选择题
1.已知方程x2-3x+1=0的两个根为x1,x2,则21 · 22=( ) .
A.3 B.6 C.8 D.2
解析▶ 由题意得
答案▶ C
2.函数f(x)=2x+2x的零点所在的区间是( ) .
A. [-2, -1] B. [-1,0]
C. [0, 1] D. [1,2]
解析▶ 因为f(x)是增函数且f(-2)=2-2+2×(-2)<0,f(-1)=2-1+2×(-1)<0,f(0)=20+0>0,所以由零点存在性定理知,函数f(x)的零点在[-1,0]内,故选B.
答案▶ B
3.函数f(x)=ln(|x|-1)+x的大致图象为( ) .
解析▶ 由题意知, |x|-1>0,则x>1或x<-1.当x>1时,f(x)=ln(x-1)+x为单调递增函数,排除B,C;当x=-2时,f(-2)=ln(|-2|-1)-2=-2<0,排除D.故选A.
答案▶ A
4.已知函数f(x)是定义在R上的偶函数,且在区间(-∞,0)上单调递增.若实数a满足f(32a-1)≥f(-3) ,则a的最大值是( ) .
A. 1 B.
解析▶ 由题意可知, -3≤32a-1≤3,解得a≤.
答案▶ D
5.已知f(x)=e|x-1 |,设a=f的大小关系是( ) .
A.a>b>c B. c>a>b
C.b>a>c D. c>b>a
解析▶ f(x)e=|x-1|的图象关于直线x=1对称,且f(x)在(1, +∞)上单调递增,又1,
∴f) ,
又f
∴f.
答案▶ B
6.设函数f(x)=的取值范围为( ) .
A. [1,2] B. [0,2]
C. [1, +∞) D. [2, +∞)
解析▶ ∵f(x)=的最小值.
由二次函数性质可得a≥1,
由分段函数性质得(1-a) 2-1≤ln 1,
解得0≤a≤2.
综上,a的取值范围为[1,2] ,故选A.
答案▶ A
7.已知函数f(x)=的取值范围是( ) .
A. 0+∞
C. 0
解析▶ 在同一坐标系内画出y=f(x) ,y=mx+m在(-1, 1]上的图象,
动直线y=mx+m过定点(-1,0) ,观察图象可知,当0<m≤21时,两图象有两个不同的交点,从而方程f(x)-mx-m=0有两个不同的实根,故选D.
答案▶ D
8.已知f(x)=2x-1,g(x)=1-x2,规定:当|f(x) |≥g(x)时,h(x)=|f(x) |;当|f(x) |<g(x)时,h(x)=-g(x) .则h(x) ( ) .
A.有最小值-1,最大值1
B.有最大值1,无最小值
C.有最小值-1,无最大值
D.有最大值-1,无最小值
解析▶ 画出y=|f(x) |=|2x-1|与y=g(x)=1-x2的图象,它们交于A,B两点.观察图象,在点A左侧,点B右侧(含A,B两点) , |f(x) |≥g(x) ,故h(x)=|f(x) |;在A,B之
间, |f(x) |<g(x) ,故h(x)=-g(x) .
综上可知,y=h(x)的图象是图中的实线部分,因此h(x)有最小值-1,无最大值,故选C.
答案▶ C
9.某食品的保鲜时间y(单位:小时)与储存温度x(单位:℃)满足函数关系y=ekx+b(e=2.718…为自然对数的底数,k,b为常数) ,若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,则该食品在33℃的保鲜时间是( )小时.
A.22 B.23 C.33 D.24
解析▶ 由题意可得,当x=0时,y=192,当x=22时,y=48.
将其代入
即有e11
则当x=33时
答案▶ D
二、填空题
10.若函数f(x)=(m+2)xa是幂函数,且其图象过点(2,4) ,则函数g(x)=l o ga (x+m)的单调递增区间为 .
解析▶ 由题设知m=-1,所以f(x)=xa,
又2a=4,所以a=2,
故g(x)=log2 (x-1) ,其单调递增区间为(1, +∞) .
答案▶ (1, +∞)
11.将甲桶中的a升水缓慢注入空桶乙中, t min后甲桶剩余的水量符合函数f(t)=aent(n为常数) .假设过5 min后甲桶和乙桶的水量相等,若再过m min后甲桶中的水只有4��升,则m的值为 .
解析▶ 因为5 min后甲桶和乙桶的水量相等,
所以函数f(t)=aen,
因此当kmin后甲桶中的水只有,解得k=10,所以m=k-5=5.
答案▶ 5
三、解答题
12.已知函数f(x)=的取值范围.
- 函数2019高考数学二轮复习第一篇微型专题微专题02函数的图象与函数的应用练习理20190313296(数理化网)相关文档
- "第二十五届全区青少年科技创新大赛参加终评答辩项目清单",,,,
- 孩子微型网
- 2017年中国技能大赛-"亚龙杯"全国智能楼宇和电梯安装维修
- 服务微型网
- "第二十五届全区青少年科技创新大赛进入终评项目清单",,,,
- 函数2019高考数学二轮复习第一篇微型专题微专题03导数及其应用练习理20190313297(数理化网)
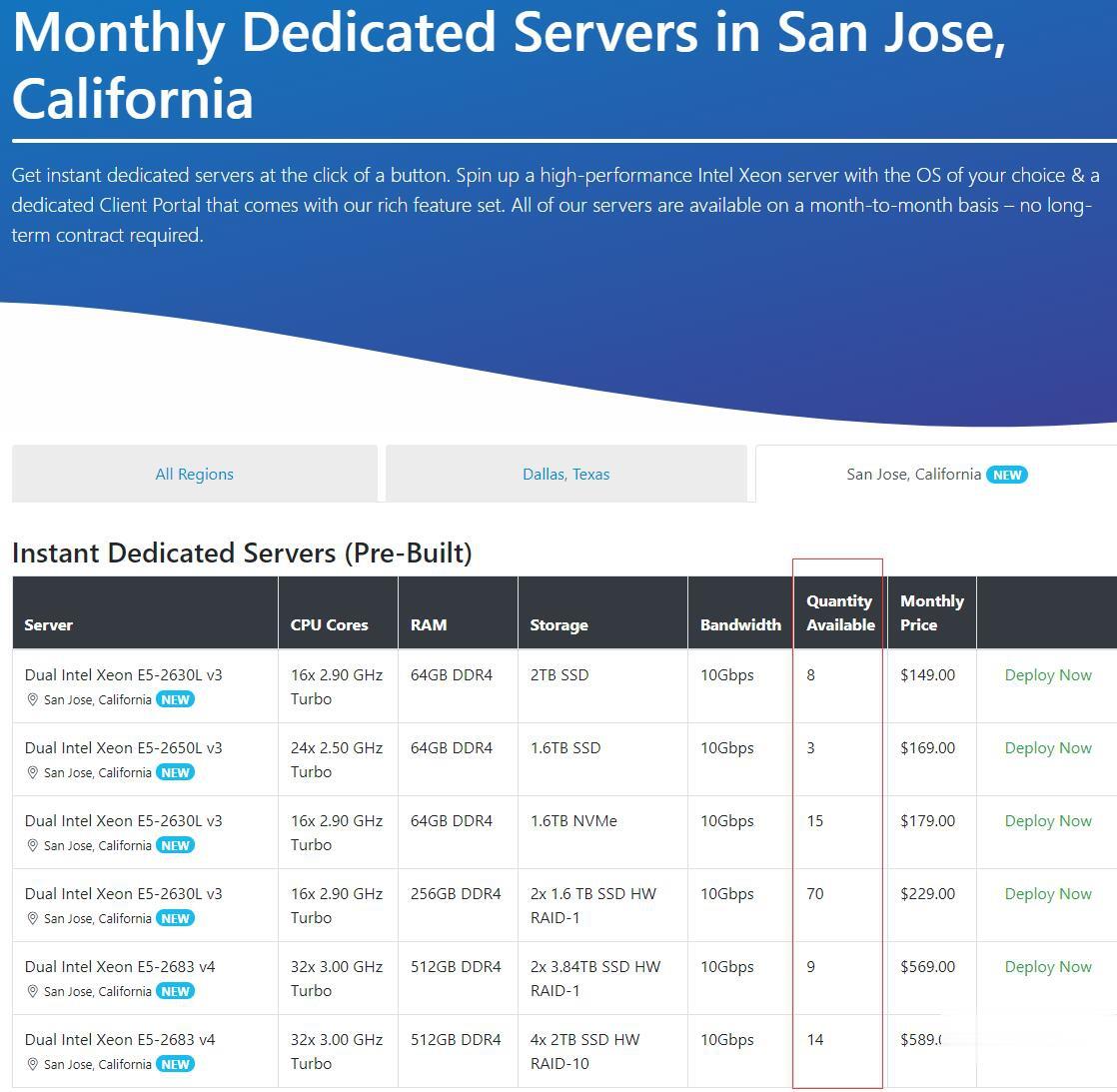
Spinservers:美国圣何塞机房少量补货/双E5/64GB DDR4/2TB SSD/10Gbps端口月流量10TB/$111/月
Chia矿机,Spinservers怎么样?Spinservers好不好,Spinservers大硬盘服务器。Spinservers刚刚在美国圣何塞机房补货120台独立服务器,CPU都是双E5系列,64-512GB DDR4内存,超大SSD或NVMe存储,数量有限,机器都是预部署好的,下单即可上架,无需人工干预,有需要的朋友抓紧下单哦。Spinservers是Majestic Hosting So...
TmhHost香港三网CN2 GIA月付45元起,美国CN2 GIA高防VPS季付99元起
TmhHost是一家国内正规公司,具备ISP\ICP等资质,主营国内外云服务器及独立服务器租用业务,目前,商家新上香港三网CN2 GIA线路VPS及国内镇江BGP高防云主机,其中香港三网CN2 GIA线路最低每月45元起;同时对美国洛杉矶CN2 GIA线路高防及普通VPS进行优惠促销,优惠后美国洛杉矶Cera机房CN2 GIA线路高防VPS季付99元起。香港CN2 GIA安畅机房,三网回程CN2 ...

易探云330元/年,成都4核8G/200G硬盘/15M带宽,仅1888元/3年起
易探云服务器怎么样?易探云是国内一家云计算服务商家,致力香港云服务器、美国云服务器、国内外服务器租用及托管等互联网业务,目前主要地区为运作香港BGP、香港CN2、广东、北京、深圳等地区。目前,易探云推出的国内云服务器优惠活动,国内云服务器2核2G5M云服务器低至330元/年起;成都4核8G/200G硬盘/15M带宽,仅1888元/3年起!易探云便宜vps服务器配置推荐:易探云vps云主机,入门型云...
-
邮箱怎么写正确的邮箱地址怎么写yy频道中心yy语音怎么进频道中心bbsxpdvbbs bbsxp LeadBBS 对比支付宝查询余额支付宝钱包怎么查余额?人人时光机现在世界上有时光机吗深圳公交车路线深圳公交线路天天酷跑刷积分教程天天酷跑积分怎么刷最快?显卡温度多少正常显卡温度多少算正常?显卡温度多少正常显卡温度多少正常网店推广网站开网店如何做推广?