floyd算法Floyd算法是什么?
floyd算法 时间:2021-06-19 阅读:()
求最短路径算法有哪几种?
原发布者:萨sky 简述几种常用的最短路径算法摘要:随着社会的发展,最短路径问题在现实生活中占据的地位越来越重要。求解这一类问题的方法有很多,包括Floyd算法、Dijkstra算法、Bellman-Ford算法、动态规划算法和智能优化算法。
其中较为常用的是Floyd算法、Dijkstra算法和Bellman-Ford算法。
本文将简单介绍这三种最短路径算法,通过比较各种方法的优劣使对其有更进一步的认识和学习。
关键字:最短路径;最短路径算法;Floyd算法;Dijkstra算法;Bellman-Ford算法随着计算机科学的发展,人们生产生活效率要求的提高,最短路径问题逐渐成为计算机科学、运筹学、地理信息科学等学科的一个研究热点。
也正因为最短路径问题在实际生产生活中应用广泛,优化该算法和提高算法的求解效率具有重大的现实意义。
1.最短路径概述最短路径问题是指在一个赋权图的两个节点之间找出一条具有最小权的路径,这是图论的描述,也是图论中研究的一个重要问题。
现实生活中我们可以看到这些最短路径问题的例子,公交车辆的最优行驶路线和旅游线路的选择等;军事领域中也有应用,作战部队的行军路线等问题就与寻找一个图的最短路径密切相关,因此对最短路径问题的深入研究和广泛应用具有重要意义和实用价值。
在线路优化问题中,如果优化指标与路程的相关性较强,而和其他因素相关性较弱时,即以最短路程为准则,则考虑转化为最短路径问题。
比如军事行军线路选取时,假如从出发地到目的地之间有多种线路可以选取,危
用Floyd算法求有向网G中各对顶点之间的最短路径
#define MAX_NAME 5 // 顶点字符串的最大长度+1 #define MAX_INFO 20 // 相关信息字符串的最大长度+1 typedef int VRType; typedef char VertexType[MAX_NAME]; typedef char InfoType; #include"c1.h" #include"c7-1.h" #include"bo7-1.cpp" typedef int PathMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM][MAX_VERTEX_NUM]; typedef int DistancMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; void ShortestPath_FLOYD(MGraph G,PathMatrix &P,DistancMatrix &D) { // 用Floyd算法求有向网G中各对顶点v和w之间的最短路径P[v][w]及其 // 带权长度D[v][w]。若P[v][w][u]为TRUE,则u是从v到w当前求得最短 // 路径上的顶点。
int u,v,w,i; for(v=0;v<G.vexnum;v++) // 各对结点之间初始已知路径及距离 for(w=0;w<G.vexnum;w++) { D[v][w]=G.arcs[v][w].adj; for(u=0;u<G.vexnum;u++) P[v][w][u]=FALSE; if(D[v][w]<INFINITY) // 从v到w有直接路径 { P[v][w][v]=TRUE; P[v][w][w]=TRUE; } } for(u=0;u<G.vexnum;u++) for(v=0;v<G.vexnum;v++) for(w=0;w<G.vexnum;w++) if(D[v][u]+D[u][w]<D[v][w]) // 从v经u到w的一条路径更短 { D[v][w]=D[v][u]+D[u][w]; for(i=0;i<G.vexnum;i++) P[v][w][i]=P[v][u][i]||P[u][w][i]; } } void main() { MGraph g; int i,j,k,l,m,n; PathMatrix p; DistancMatrix d; CreateDN(g); for(i=0;i<g.vexnum;i++) g.arcs[i][i].adj=0; // ShortestPath_FLOYD()要求对角元素值为0 printf("邻接矩阵: "); for(i=0;i<g.vexnum;i++) { for(j=0;j<g.vexnum;j++) printf("%11d",g.arcs[i][j]); printf(" "); } ShortestPath_FLOYD(g,p,d); printf("d矩阵: "); for(i=0;i<g.vexnum;i++) { for(j=0;j<g.vexnum;j++) printf("%6d",d[i][j]); printf(" "); } for(i=0;i<g.vexnum;i++) for(j=0;j<g.vexnum;j++) printf("%s到%s的最短距离为%d ",g.vexs[i],g.vexs[j],d[i][j]); printf("p矩阵: "); l=strlen(g.vexs[0]); // 顶点向量字符串的长度 for(i=0;i<g.vexnum;i++) { for(j=0;j<g.vexnum;j++) { if(i!=j) { m=0; // 占位空格 for(k=0;k<g.vexnum;k++) if(p[i][j][k]==1) printf("%s",g.vexs[k]); else m++; for(n=0;n<m*l;n++) // 输出占位空格 printf(" "); } else for(k=0;k<g.vexnum*l;k++) // 输出占位空格 printf(" "); printf(" "); // 输出矩阵元素之间的间距 } printf(" "); } }
Floyd算法是什么?
Floyd算法又称为弗洛伊德算法,插点法,是一种用于寻找给定的加权图中顶点间最短路径的算法。通过一个图的权值矩阵求出它的每两点间的最短路径矩阵。
从图的带权邻接矩阵A=[a(i,j)] n×n开始,递归地进行n次更新,即由矩阵D(0)=A,按一个公式,构造出矩阵D(1);又用同样地公式由D(1)构造出D(2);……;最后又用同样的公式由D(n-1)构造出矩阵D(n)。
矩阵D(n)的i行j列元素便是i号顶点到j号顶点的最短路径长度,称D(n)为图的距离矩阵,同时还可引入一个后继节点矩阵path来记录两点间的最短路径。
采用的是(松弛技术),对在i和j之间的所有其他点进行一次松弛。
所以时间复杂度为O(n^3); 其状态转移方程如下: map[i,j]:=min{map[i,k]+map[k,j],map[i,j]} map[i,j]表示i到j的最短距离 K是穷举i,j的断点 map[n,n]初值应该为0,或者按照题目意思来做。
当然,如果这条路没有通的话,还必须特殊处理,比如没有map[i,k]这条路
- floyd算法Floyd算法是什么?相关文档
- floyd算法求matlab高手,帮我解决一下floyd算法!!急急急
- floyd算法谁可以给我讲一下floyd算法吗?
- floyd算法【讨论】最短路径弗洛伊德算法的时间复杂度?
- floyd算法Floyd算法的优缺点分析
- floyd算法比较Dijkstra算法与Floyd算法。
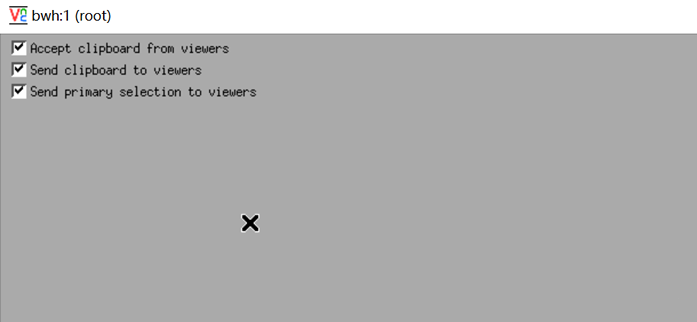
远程登录VNC无法连接出现
今天有网友提到自己在Linux服务器中安装VNC桌面的时候安装都没有问题,但是在登录远程的时候居然有出现灰色界面,有三行代码提示"Accept clipboard from viewers,Send clipboard to viewers,Send primary selection to viewers"。即便我们重新登录也不行,这个到底如何解决呢?这里找几个可以解决的可能办法,我们多多尝试。...
注册做什么96%可以干啥,常用的7个常用的国内国外域名注册服务商_云服务器可以干什么
日前,国内知名主机服务商阿里云与国外资深服务器面板Plesk强强联合,推出 阿里云域名注册与备案、服务器ECS购买与登录使用 前言云服务器(Elastic 只需要确定cpu内存与带宽基本上就可以了,对于新手用户来说,我们在购买阿里云服务申请服务器与域名许多云服务商的云服务器配置是弹性的 三周学会小程序第三讲:服务 不过这个国外服务器有点慢,可以考虑国内的ngrokcc。 ngrokcc...

hosteons:10Gbps带宽,免费Windows授权,自定义上传ISO,VPS低至$21/年,可选洛杉矶达拉斯纽约
hosteons当前对美国洛杉矶、达拉斯、纽约数据中心的VPS进行特别的促销活动:(1)免费从1Gbps升级到10Gbps带宽,(2)Free Blesta License授权,(3)Windows server 2019授权,要求从2G内存起,而且是年付。 官方网站:https://www.hosteons.com 使用优惠码:zhujicepingEDDB10G,可以获得: 免费升级10...
floyd算法为你推荐
-
允许traceroute探测移动基站辐射国家允许范围是多少?怎么检测?建行手机网站建设手机银行首次怎样登录scriptmanagerscriptmanager.registerstartupscript是.net3.5吗ico监管ICO为什么被叫停excel大写金额在EXCEL表格里怎样自动生成金额大写sdfsdfsdfsdf小米手机投诉热线pat是什么格式如何把JPG图片变为PAT格式图片?手机软件开发工具如何自己开发一个app软件5e5e5e计算器里5.55556e-5是什么意思java程序员招聘女java程序员好找工作嘛