线性规划问题运筹学线性规划问题
关于数学简单的线性规划问题的讲解
近年来,各级各类数学竞赛中频频出现线性规划问题。
所谓线性规划,是指求线性函数在线性(不等式或等式)约束下达最(小或大)值的问题。
线性规划广泛应用于工农业、军事、交通运输、决策管理与规划、科学实验等领域。
本文拟通过竞赛试题介绍常用的解题思路和方法。
一、运用数量关系解题
例1某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按120个工时计算)生产空调器、彩电、冰箱共360台,且冰箱至少生产60台。
已知生产这些家电产品每台所需工时和每台产值如下表:
问每周应生产空调器、彩电、冰箱各多少台,才能使产值最高?最高产值是多少(以千元为单位)?
(1997,第十二届江苏省初中数学竞赛)
解:设每周生产空调器、彩电、冰箱分别为x台、y台、z台,每周产值为f元,则
f=4x+3y+2z.
其中x、y、z满足
由①、②得y=360—3x,z=2x.
则由
得30≤x≤120.
故f=3(x+y+z)+x—z=1080—x.
当x=30时,fmax=1080—30=1050.
从而,y=270,z=60.
即每周生产空调器30台,彩电270台,冰箱60台,才能使产值最高,最高产值为1050千元。
二、运用图表作业解题
例2A市、B市和C市分别有某种机器10台、10台和8台。
现在决定把这些机器支援给D市18台、E市10台。
已知从A市调运一台机器到D市、E市的运费分别为200元和800元;从B市调运一台机器到D市、E市的运费分别为300元和700元;从C市调运一台机器到D市、E市的运费分别为400元和500元。
⑴设从A市、B市各调x台机器到D市,当28台机器全部调运完毕后,求总运费W(元)关于x(台)的函数式,并求W的最小值和最大值;
⑵设从A市调x台到D市,B市调y台到D市,当28台机器全部调运完毕后,用x、y表示总运费W(元),并求W的最小值和最大值。
(1998,全国初中数学竞赛)
解:⑴⑵这两问都可以运用数量关系解题,具体解法参见《中等数学》1998年第3期第34页或1999年第4期第3页文。
下面以第⑵问为例说明运用图表作业解题。
⑵(表上作业法)
由题意,易得W(x,y)=17200—500x—300y.
Ⅰ.求最小总运费Wmin.
表中对于D市、E市可供货的A、B、C三地进行比较,逐次选取较小运费地,尽可能的调运,得调运方案如表1所示:
即当x=10,y=8时,最小总运费Wmin=9800(元)。
Ⅱ.求最大总运费Wmax.
类似地,可得调运方案如表2所示:
即当x=0,y=10时,最大总运费Wmax=14200(元)。
(图上作业法)
由题意,易得W(x,y)=17200—500x—300y.
Ⅰ.求最小总运费Wmin.
图中所标运费可以看作是单位运量。
供量用正数表示,需量则用负数表示,对于D市、E市可供货的A、B、C三地进行比较,逐次选取单位运量较小的,尽可能的调运,得调运方案如图1所示:
即当x=10,y=8时,最小总运费Wmin=9800(元)。
Ⅱ.求最大总运费Wmax.
类似地,可得调运方案如图2所示:
即当x=0,y=10时,最大总运费Wmax=14200(元)。
三、运用图象性质解题
例3某工厂制造A、B两种产品,制造产品A每吨需用煤9吨,电力4千瓦,3个工作日;制造产品B每吨需用煤5吨,电力5千瓦,10个工作日。
已知制造产品A和B每吨分别获利7千元和12千元,现在该厂由于条件限制,只有煤360吨,电力200千瓦,工作日300个可以利用,问A、B两种产品各应生产多少吨才能获利最大?最大利润是多少?
解:设A、B两种产品分别生产x吨、y吨,利润为f千元,则
f=7x+12y.
其中x、y满足
如图3所示,阴影部分即为这个线性规划问题的可行区域。
∵—4/5<—7/12<—3/10,
∴平行直线系f=7x+12y过点A(20,24)即当x=20,y=24时,fmax=7×20+12×24=140+288=428(千元)。
即产品A生产20吨,产品B生产24吨,获利最大,最大利润为428千元。
四、运用枚举验证解题
例4某人有楼房一幢,室内面积共180m2,拟分隔成两类房间作为旅游客房。
大房间每间面积为18m2,可住游客5名,每名游客每天住宿费为40元;小房间每间面积为15m2,可住游客3名,每名游客每天住宿费为50元;装修大房间每间需1000元,装修小房间每间需600元。
如果他只能筹款8000元用于装修,且游客能住满客房,他应隔出大房间和小房间各多少间,能获得最大收益?最大收益是多少?
解:设隔出大、小房间分别为x间、y间,收益为f元,则
f=200x+150y.
其中x、y满足
如图4所示,由图解法易得f=200x+150y过点A(23/7,63/7)时,目标函数f取得最大值。
但x、y必须是整数,还需在可行区域内找出使目标函数f取得最大值的整点。
显然目标函数f取得最大值的整点一定是分布在可行区域的右上侧,则利用枚举法即可求出整点最优解。
这些整点有:(0,12),(1,10),(2,9),(3,8),(4,6),(5,5),(6,3),(7,1),(8,0),分别代入f=200x+150y,逐一验证,可得取整点(0,12)或(3,8)时,fmax=200×0+150×12=200×3+150×8=1800(元)。
所以要获得最大收益,有两种方案:
Ⅰ.只隔出小房间12间;
Ⅱ.隔出大房间3间,小房间8间。
最大收益为1800元
线性规划问题的解法有哪几种
1.目标函数是无数条平等线,也就是书中的主流线列数条平行线, 2,过一点的无数条相交线,如Z=(y-3)/(x+1)这一类问题 3.格点问题也就是整数点的问题 4动圆的半径Z=√X^2+Y^2线性规划问题的特征是什么?
、每个模型都有若干个决策变量(x1,x2,x3……,xn),其中n为决策变量个数。
决策变量的一组值表示一种方案,同时决策变量一般是非负的。
2、目标函数是决策变量的线性函数,根据具体问题可以是最大化(max)或最小化(min),二者统称为最优化(opt)。
3、约束条件也是决策变量的线性函数。
当我们得到的数学模型的目标函数为线性函数,约束条件为线性等式或不等式时称此数学模型为线性规划模型。
线性规划问题数学模型的三个要素是什么
线性规划问题的形式特征,三个要素组成: 1、变量或决策变量; 2、目标函数; 3、约束条件。求解线性规划问题的基本方法是单纯形法,已有单纯形法的标准软件,可在电子计算机上求解约束条件和决策变量数达 10000个以上的线性规划问题。
为了提高解题速度,又有改进单纯形法、对偶单纯形法、原始对偶方法、分解算法和各种多项式时间算法。
对于只有两个变量的简单的线性规划问题,也可采用图解法求解。
这种方法仅适用于只有两个变量的线性规划问题。
它的特点是直观而易于理解,但实用价值不大。
通过图解法求解可以理解线性规划的一些基本概念。
扩展资料: 线性规划建立的数学模型具有以下特点: 1、每个模型都有若干个决策变量(x1,x2,x3……,xn),其中n为决策变量个数。
决策变量的一组值表示一种方案,同时决策变量一般是非负的。
2、目标函数是决策变量的线性函数,根据具体问题可以是最大化(max)或最小化(min),二者统称为最优化(opt)。
3、约束条件也是决策变量的线性函数。
当我们得到的数学模型的目标函数为线性函数,约束条件为线性等式或不等式时称此数学模型为线性规划模型。
参考资料来源:搜狗百科-线性规划
运筹学线性规划问题
设x为投资第一种的金额,y为投资第二种的金额。则目标方程是max=1.7*x*3+3*y(1式),约束条件是x+y=100000(2式)。
把2式变形后带入1式,求一个一元函数的最大值就行了。
可以用倒数法求最大值。
具体值自己再算算吧。
- 线性规划问题运筹学线性规划问题相关文档
- 线性规划问题什么是线性规划问题,及有那些相关概念?如何解决
- 线性规划问题名词解释:1,线性规划问题的基解 ? 2,线性规划问题的最优解? 谢谢
- 线性规划问题简述“线性规划问题”?并举例说明线性规划问题图解法的基本原理?
- 线性规划问题运筹学线性规划题
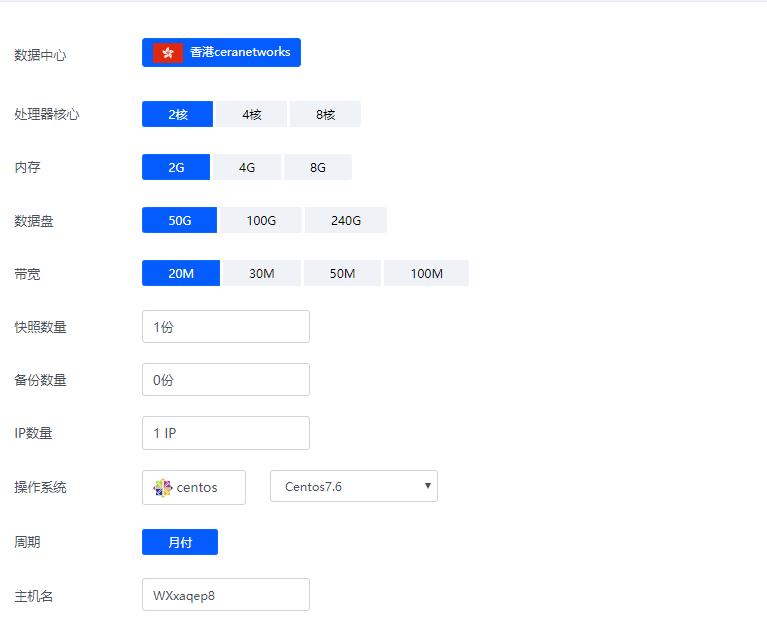
香港ceranetworks(69元/月) 2核2G 50G硬盘 20M 50M 100M 不限流量
香港ceranetworks提速啦是成立于2012年的十分老牌的一个商家这次给大家评测的是 香港ceranetworks 8核16G 100M 这款产品 提速啦老板真的是豪气每次都给高配我测试 不像别的商家每次就给1核1G,废话不多说开始跑脚本。香港ceranetworks 2核2G 50G硬盘20M 69元/月30M 99元/月50M 219元/月100M 519元/月香港ceranetwork...
香港站群多ip服务器多少钱?零途云香港站群云服务器怎么样?
香港站群多ip服务器多少钱?想做好站群的SEO优化,最好给每个网站都分配一个独立IP,这样每个网站之间才不会受到影响。对做站群的站长来说,租用一家性价比高且提供多IP的香港多ip站群服务器很有必要。零途云推出的香港多ip站群云服务器多达256个IP,可以满足站群的优化需求,而且性价比非常高。那么,香港多ip站群云服务器价格多少钱一个月?选择什么样的香港多IP站群云服务器比较好呢?今天,小编带大家一...

2021年7月最新洛杉矶CN2/香港CN2 vps套餐及搬瓦工优惠码 循环终身优惠6.58%
搬瓦工怎么样?2021年7月最新vps套餐推荐及搬瓦工优惠码整理,搬瓦工优惠码可以在购买的时候获取一些优惠,一般来说力度都在 6% 左右。本文整理一下 2021 年 7 月最新的搬瓦工优惠码,目前折扣力度最大是 6.58%,并且是循环折扣,续费有效,可以一直享受优惠价格续费的。搬瓦工优惠码基本上可能每年才会更新一次,大家可以收藏本文,会保持搬瓦工最新优惠码更新的。点击进入:搬瓦工最新官方网站搬瓦工...
-
技术文档管理文档管理的步骤?融360我想申请(融360)贷款5万元,一年得付多少利息?eofexceptionjava.io.EOFException这是个什么异常应该怎么解决fast路由器FAST/迅捷无线路由器怎么设置什么是cookie覆盖自动cookie处理是什么意思活跃网络十大网络家族排行榜详情监控员工公司如何监控员工手机和微信硬盘分区格式化如何将电脑里的所有硬盘分区全部格式化?硬盘分区格式化硬盘分区后怎么格式化摇一摇周边什么是微信摇一摇周边?